2021年度国税専門官3

あるパン屋では、パンを毎日同じ数だけ作り、その日のうちに売り切っている。　　　　　　　　　　　　　　　　　　昨日は、200円で24個販売したところで半額に値下げして、全て売り切った。　　　　　　　　　　　　　　　　　　今日は、200円で全体の3/8を販売したところで150円に値下げし、残りが全体の1/8になったところで100円に値下げして、全て売り切った。　　　　　　　　　　　　　　　　　　昨日半額で販売した数と今日150円で販売した数が同じであったとき、昨日と今日の売上げの差は何円か。　　　　　　　　　　　　　　　　　　①300円　②400円　③500円　④600円　⑤700円　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　「あるパン屋では、パンを毎日同じ数だけ作り、その日のうちに売り切っている。」とありますから、昨日も今日も、売ったパンの個数は同じです。　　　　　　　　　　　　　　　　　　　今日の販売状況から確認します。全体を8k個とすると、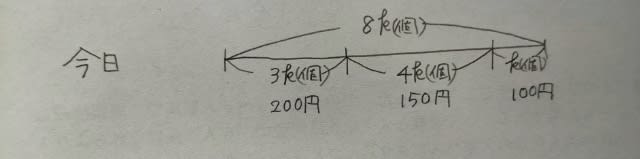
昨日の販売状況ですが、「昨日半額で販売した数と今日150円で販売した数が同じであった」とありますから、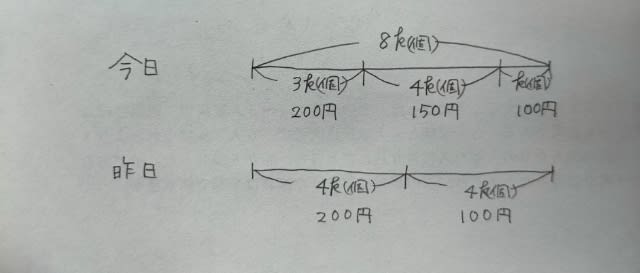
「昨日は、200円で24個販売したところで150円に値下げし、」とあります。　　　　　　　　　　　　　　　　　　　よって、4k＝24。つまりk＝6ですね。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　昨日の売り上げは、200×4k＋100×4kを計算して1200k円。　　　　　　　　　　　　　　　　　　　今日の売り上げは、200×3k＋150×4k＋100×kを計算して1300k円。　　　　　　　　　　　　　　　　　　　その差は100k円。k＝6なので、600円。　　　　　　　　　　　　　　　　　　　正解は、肢④です。ここをポチッとお願いします。→

にほんブログ村

2019年地方上級5

誕生日が同じAとBの2人がいる。AはBよりも年下であり、Aの年齢が現在のBの年齢に達するとき、Bの年齢はAの年齢の1.2倍となる。かつて、Bの年齢が現在のAの年齢であったときは、Aの年齢とBの年齢の和は42であった。AとBの年齢の差はいくらか。　　　　　　　　　　　　　　　　　　①4　②6　③8　④10　⑤12　　　　　　　　　　　　　　　　　　　過去と現在と未来の話です。表に整理して考えます。現在のAの年齢をa、Bの年齢をbとします。
2人の誕生日は同じだから、いつでも年齢差は同じです。つまり、いつでも(Bの年齢)−(Aの年齢)は等しい。よって、
さて、ここからどうするかは、2派に分かれそうです。まず、数学派のやり方。
次に、算数派のやり方。
正解は、肢②です。ここをポチッとお願いします。→

にほんブログ村

不定方程式。地方上級。

ある洋菓子店には3種類のケーキＡ〜Ｃがあり、1個の値段はＡが300円、Ｂが200円、Ｃが150円である。Ａ〜Ｃのケーキをそれぞれ偶数個ずつ合計で16個買ったところ、代金は3000円であった。このとき、買ったケーキの個数について正しくいえることは、次のうちどれか。ただし、どれも少なくとも2個は買ったものとし、税は考えないものとする。　　　　　　　　　　　　　　　　　　　①ＡはＢより4個少なかった。　　　　　　　　　　　　　　　　　　　②ＡはＣより4個少なかった。　　　　　　　　　　　　　　　　　　　③ＢはＡより4個少なかった。　　　　　　　　　　　　　　　　　　　④ＢはＣより4個少なかった。　　　　　　　　　　　　　　　　　　　⑤ＣはＢより4個少なかった。　　　　　　　　　　　　　　　　　　　典型的な不定方程式の問題ですね。条件を整理すると、
ここから、方程式が2つできます。
ガンガン行きます。
条件より、a、b、cは、全て偶数で、0はダメ。よって、
もうこれは、Ａを2個、Ｂを6個、Ｃを8個買うしかないようですね。正解は、肢①です。ここをポチッとお願いします。→
にほんブログ村

１個あたり、１分あたり。平成３０年度国家一般職(大卒)

ある工場では、２種類の製品Ａ、Ｂを製造しており、その製造に要する時間は、それぞれ１個あたり、常に次のとおりである。


ある日、この工場では、合計６０人の作業員を製品Ａ、Ｂのいずれか一方の製造の担当に振り分けて同時に製造を開始したところ、４時間後の時点で、この日に製品Ｂを製造した個数がちょうど３５個となり、製造を一時停止した。製品Ａの製造を担当する作業員を新たに何人か追加して製造を再開したところ、再開して２時間２０分後に、この日に製品Ａを製造した個数がちょうど８０個となり製造を終了した。この日、製品Ａの製造を担当する作業員を新たに追加した後、製品Ａの製造を行っていた作業員の人数は何人か。　　　　　　　　　　　　　　　　　　　　　ただし、作業員は、担当となった種類の製品の製造のみを行うものとする。　　　　　　　　　　　　　　　　　　　　1. 28人　　2. 30人　　3. 32人　　　4. 34人　　　5. 36人　　　　　こんなことですね。

まず、Ｂですが、４時間(２４０分)で３５個製造したのだから、

よって、Ａを担当したのは、60−35＝25人でした。そして、この４時間で、Ａは５０個製造されています。

再開後の２時間２０分で、Ａは80−50＝30個製造されたのだから、

正解は、肢２です。　　　　　　　　　　　　　　　　　　　　　本問は、１個何分か？１分何個か？何個で何分か？何分で何個か？が、ランダムに出てきます。　　　　　　　　　　　　　　　　　　　　　(個)や（分)といった、単位をよく考えていかないと、頭の中がごちゃごちゃになってしまいますね。ここをポチッとお願いします。→
にほんブログ村

平成30年度警察官8

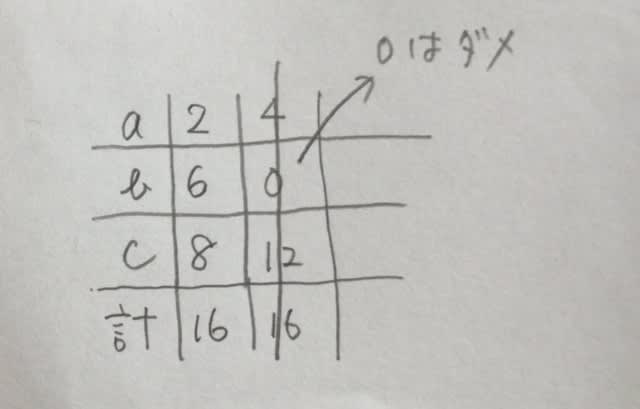
A～Cはリンゴ狩りに行った。A～Cが採ったリンゴの個数について、次のことが分かっているとき、AとBの採ったリンゴの個数の比に当てはまるのはどれか。　　　　　　　　　　　　　　　　　　　　　・AはBより10個多く採り、Cより17個多く採った。　　　　　　　　　　　　　　　　　　　　　・Aの採ったリンゴの個数はCの採ったリンゴの個数の3倍より多かった。　　　　　　　　　　　　　　　　　　　　　・Bの採ったリンゴの個数はCの採ったリンゴの個数の2倍よりは少なかった。条件を式で表すと、A＝B＋10…①　　　　　　　　　　　　　　　　　　　　A＝C＋17…②　　　　　　　　　　　　　　　　　　　　A＞3C…③　　　　　　　　　　　　　　　　　　　　B＜2C…④　　　　　　　　　　　　　　　　　　　　②を③に代入すると、Cだけの不等式になります。次に、④の不等式を、Cだけの不等式にできないかを考えます。①式と②式を使って、BとCの方程式にすれば、うまくいきます。C＜8.5かつC＞7で、Cは整数なので、C＝8です。　　　　　　　　　これを②式に代入して、A＝8＋17＝25。　　　　　　　　　　　　　　　　　　　これを①式に代入して、25＝B＋10。ゆえにB＝15。A：Bは、25：15で、簡単にすると5：3。正解は、肢5です。ここをポチッとお願いします。→
にほんブログ村