警視庁Ⅲ類の数的推理 2

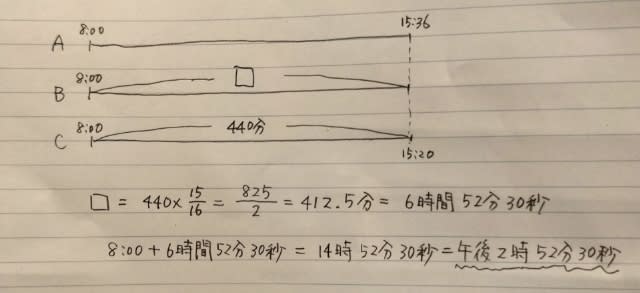
2021年出題。　　　　　　　　　　　　　　　　　　　　　　　　　次の図で、4ヶ所を赤、青、黄、緑の4色の色鉛筆を用いて、隣り合う部分が異なる色になるように塗り分けるとき、塗り分け方の総数として、最も妥当なのはどれか。ただし、使わない色があってもよいものとする。（選択肢省略）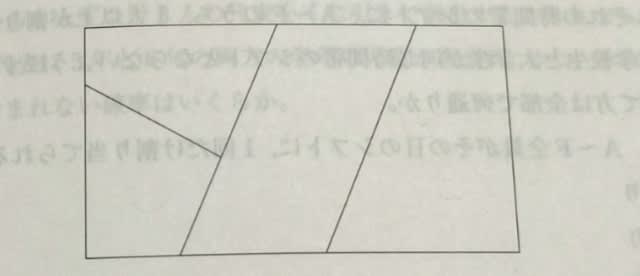
隣り合う部分が異なる色になるようにするので、下図のア、イ、ウは、全て異なる色を塗らなければなりません。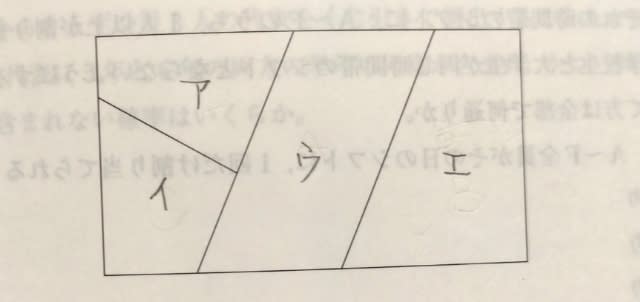


アが4通り、イは3通り、ウは2通りなので、4×3×2=24通り。　　　　　　　　　　　　　　　　　　最後にエに色を塗ります。　　　　　　　　　　　　　　　　　エは、ウに塗った色以外の色を塗るので、3通り。　　　　　　　　　　　　　　　　　　　　　　よって、塗り方の総数は、24×3=72通り。　　　　　　　　　　　　　　　　　　　　　　　　正解は、72通りです。

中学入試に学ぶ 2

今回は、旅人算です。　　　　　　　　　　　　　　　初級〜中級対象でしょうか。　　　　　　　　　　　問題。　　　　　　　　　　　　　　　　　　　　　　　　　　　海子さんは家から学校まで毎時3kmの速さで歩いていきました。　　　　　　　　　　　　　　　　海子さんが出てから12分後にお母さんは忘れ物を届けに自転車に乗って毎時13kmの速さで追いかけたところ、学校までの道のりの5分の3の地点で海子さんに追いつきました。　　　　　　　　　　　　　　　　　　　　　海子さんの家から学校までの道のりは□kmです。　　　　　　　　　　　　　　　　　　　　　　　まずは、大人の考え方で解いてみます。　　　　　　　　　　　　　12分=12/60=1/5時間だから、海子さんが出発してから12分で進む距離は、3×1/5=3/5km。　　　　　　　　　　　　　　　　　　　　　　　お母さんが出発してからt時間後に海子さんに追いつくとして、方程式を作ります。
よって、家から39/50km地点でお母さんは海子さんに追いつきます。
家から学校までの距離をx（km）とすると、題意より、3/5×x=39/50。　　　　　　　　　　　　　　　これを解いて、x=1.3。　　　　　　　　　　　　　　　　正解は、1.3です。　　　　　　　　　　　　　　　　　　何か分数が多いですね。　　　　　　　　　　　　　　　　　　これを小学生はどう解くか?　　　　　　　　　　　　　　「速さの比」に注目します。　　　　　　　　　　　　　　　　海子さんの速さ:お母さんの速さ=3:13であり、お母さんが出発してから海子さんに追いつくまでは、二人は同じ時間進んでいます。
同じ時間進んだのだから、その距離は、速さの比と同じく3:13。（速ければ速いほどたくさん進みます）よって、
海子さんが12分で進んだ距離は、⑬−③=⑩ですね。
少し寄り道をします。　　　　　　　　　　　　　　　　　　　　我々が普通に歩いているときの速さは、約4㎞/時。　　　　　　　　　　　　　　　　　　　　　　　　早足で歩くと、約6㎞/時です。　　　　　　　　　　　　　　　この6㎞/時は、ちょうど100m/分。　　　　　　　　　　　つまり、100mをちょうど1分で進もうと思えば、早足で歩けばよいのです。　　　　　　　　　　　　これは、速さの問題を解くときに便利なので、是非覚えて下さい。　　　　　　　　　　　　　　　　　海子さんは、おそらく小学3年生くらいでしょう。　　　　　　　　　　　　　　　　　　　　　　　　　　6㎞/時の半分の速さで歩いているので、50m/分です。　　　　　　　　　　　　　　　　　　　　　　　　この速さで12分進むと、50×12=600m進んでいます。　　　　　　　　　　　　　　　　　　　　　よって、
この780mが、学校までの道のりの3/5ですから、
大人の場合は、⑬や③は、13k、3kなどと文字を使って、方程式をたてたりすればよいかと思います。

警視庁Ⅲ類の数的推理 1

2021年出題。　　　　　　　　　　　　　　　　　　　　　A、B、Cの3人が、3kmのハイキングコースを歩くことになった。　　　　　　　　　　　　　　　　　　　Aが8歩進む時間の間にBはちょうど6歩進み、Cはちょうど5歩進む。　　　　　　　　　　　　　　　　　また、Aが5歩で進む距離をBはちょうど4歩で進み、Cはちょうど3歩で進む。　　　　　　　　　　　　　　　　スタート地点からこの3人が同時に歩き始め、誰かが最初にゴール地点に到達したとき、まだゴール地点に到達していない残りの2人の間の距離として、最も妥当なのはどれか。（選択肢省略）　　　　　　　　　　　　　　　　　　ピッチの比×歩幅の比=速さの比　という公式を知っている人は、こうです。　　　　　　　　　　　　　　　　問題文中、「Aが8歩進む時間」とありますが、この時間内にAは8回、Bは6回、Cは5回足を動かすので、ピッチの比はA:B:C=8:6:5。　　　　　　　　　　　　　　　　　　　　　　　　　　　　「Aが5歩で進む距離」とありますが、この距離を1とすると、Aの歩幅は1/5、Bの歩幅は1/4、Cの歩幅は1/3。　　　　　　　　　　　　　　　　　よって、
上の公式を知らない人は、こうですね。　　　　　　　　　　　　　　Aが8歩進む時間を1秒、Aが5歩で進む距離を1mと仮定して、
この結果より、それぞれの速さは、　　　　　　　　　　　　　　Aが8/5m/秒、Bが6/4m/秒、Cが5/3m/秒。
上の表と同じですね。　　　　　　　　　　　　　　　　　　　では、その先にいきます。　　　　　　　　　　　　　　　　　　後半で出てきたA、B、Cの速さをそのまま使うと、このようになります。　　　　　　　　　　　　　　3人の速さを比べるとCが一番速い。　　　　　　　　　　　　　Cがゴールするまでにかかる時間は、3000(m)÷5/3(m/秒)=1800秒。　　　　　　　　　　　　　　　AとBでは、Aの方が0.1m/秒速い。　　　　　　　　　　　　　　　AとBが1800秒進むと、0.1×1800=180mの差ができる。　　　　　　　　　　　　　　　　　　　　よって、正解は180mです。　　　　　　　　　　　　　　　　前半のやり方で、3人の速さの比がA:B:C=48:45:50であることを使うと、
速さが48:45:50で、3人とも同じ時間進むので、進んだ距離も同じく48:45:50になるので、上の画像のようになります。















HADOアイドルウォーズ　コスモスCUP 3rdシーズン　2022.9.5　1:07〜約45分　第2試合。

中学入試に学ぶ 1

公務員試験と中学入試は似ています。　　　　　　　　　　　　　　大人が必死に解いているのを嘲笑うが如く、ほんの数十秒で正解を導き出す子供がいます。　　　　　　　　　　　　　　　　　　　　　その考え方やテクニックは、とても参考になりますので、紹介していきます。　　　　　　　　　第1回は、神戸女学院中学の過去問です。　　　　　　　　　　　　　　　　　これは大卒国家総合職、国家一般職向けです。　　　　　　　　　　　　　　　　　　　　　　　　　　針の進む速さの異なる3つの時計A、B、Cがあります。　　　　　　　　　　　　　　　　　　　　この3つの時計を同時に午前8時に合わせて動かし始めました。　　　　　　　　　　　　　　　　　　　時計Aが午前8時38分を指してから、時計Cが午前8時38分を指すまでの間に時計Bでは1分15秒経過していました。　　　　　　　　　　また、時計Aが午後3時36分ちょうどを指したとき、時計Cは午後3時20分ちょうどを指していました。　　　　　　　　　　　　　　　　　各時計の針の進む速さは一定とします。　　　　　（1）時計BとCの針の進む速さの比をもっとも簡単な整数の比で表しなさい。　　　　　　　　　　　　　　（2）時計Aが午後3時36分ちょうどを指したとき、時計Bが指している時刻を求めなさい。　　　　　　　　　　　　　　　　　　　　　　　　　まあ、こういうことですねえ。
Aが8:00〜15:36まで、7時間36分進んだ間に、Cは8:00〜15:20まで、7時間20分進んでいますね。　　　　　　　　　　　　　　　　　　　だから？　　　　　　　　　　　　　　　　　　　　　　　　　　この「だから？」に対して、たくさん語ることができる人ほど、上級者です。　　　　　　　　　　　　　知能は、一つの出来事を、どれだけ多面的に解析できるかが鍵なのです。　　　　　　　　　　　　　　　この場合は、例えば、　　　　　　　　　　　　　　　　　　Aの進む速さ:Cの進む速さ=456分:440分　　　　　　　　　　　　　だから、これを簡単な比にして、つまり57:55だということがいえます。　　　　　　　　　　　　　　　　　　　　　　　この種の問題を解くときによくこの比を使います。　　　　　　　　　　　　　　　　　　　　　　　　ただし、その方向で考えていけば、かなりややこしい計算をしなければなりません。（実際にやってみて下さい）　　　　　　　　　　　　　　そこで、もっと違う角度から。　　　　　　　　　　　　　何かありますか?　　　　　　　　　　　　　　　　　　　　　　　本気で勉強している人は、3分間考えて見てください。　　　　　　　　　　　　　　　　　　　　　こんなのはどうでしょうか?　　　　　　　　　　　　　　　　　　Aが456分進むと、Cはそれより16分遅れる。　　　　　　　　　　　　　　　　　　　　　　　　　　　とすると、Aが8:00〜8:38まで38分進むと、Cは何分遅れるか?
4/3分=1分20秒だから、Aが8:38のとき、Cはそれより1分20秒遅れ、8時36分40秒です。　　　　　　　　　　　　　　　　　　　　　　実はこの8時36分40秒は考えなくてもOK。　　　　　　　　　　　　　　　　　　　　　　　　　なぜなら、（1）では、BとCの針の進む速さを求めるだけだからです。
（1）の正解は、15:16です。　　　　　　　　　　　　　　（2）は、少し視点を変えるといいでしょう。　　　　　　　　　　　　　　　　　　　　　　　　　Aが午後3時36分ちょうどを指したとき、Bが指している時刻を求めなさいと言われましたが、これなら今度はAの進む速さとBの進む速さの比を求めにいかなければなりません。　　　　　　　　　　　　　　　　　　　　　　　しかし、上の図を見れば分かるように、この問いは、Cが午後15時20分ちょうどを指したとき、Bが指している時刻を求めなさいと同じ意味ですね。（こんなの小学生にやらせるな！）　　　　　　　　　　　　　　　　　それなら（1）の結果が使えます。　　　　　　　　　　　　　（1）より、Bが進む速さは、Cが進む速さの15/16であることが分かります。（分からなければ、別の手があるので後述）　　　　　　　　　　　　　　　　　　　　　　　　　　Cが8:00〜15:20まで440分進むと、Bは、その15/16、412.5分進みます。　　　　　　　　　　　　　つまり、14時52分30秒、正解は、午後2時52分30秒です。
さて、15/16がちょっと分からない場合は、比の式を使いましょう。こんな感じですね。