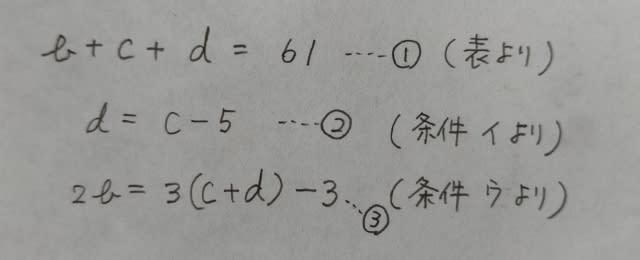ある学校にはA、B、Cの3組で合計100

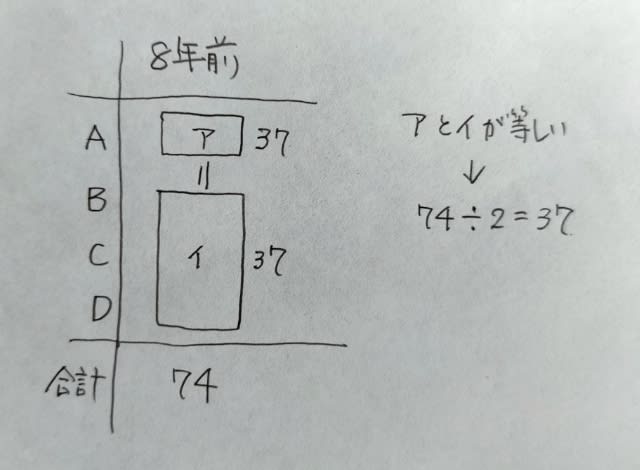
人の生徒が在籍しており、これらの生徒に対し、試験を2回実施した。1回目の試験において、100人全員が受験したところ、A組とB組では同じ人数の生徒が合格し、C組では生徒全員が不合格であった。その結果、1回目の試験で不合格であった生徒の人数比は、A組:B組:C組=1:2:4であった。 2回目の試験において、1回目の試験で不合格であった生徒を対象とし、対象者全員が受験したところ、A組では受験した生徒の80%が、B組では受験した生徒の90%が、C組では生徒全員が合格した。その結果、2回目の試験で不合格であった生徒は、A組とB組合計4人であった。 このとき、A組で2回目の試験で合格した生徒は、A組の生徒全員の何%を占めているか。①32%②34%③36%④38%⑤40% ややこしい話ですが、1回目の試験の結果を線分図で表して見ると、すっきり見えて来ますよ。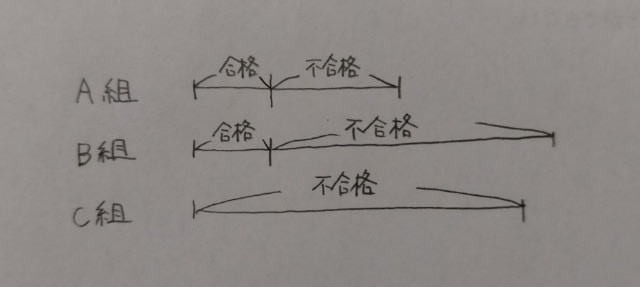
1回目の試験では、A組とB組では同じ人数の生徒が合格し、不合格であった生徒の人数比はA組:B組:C組=1:2:4なので、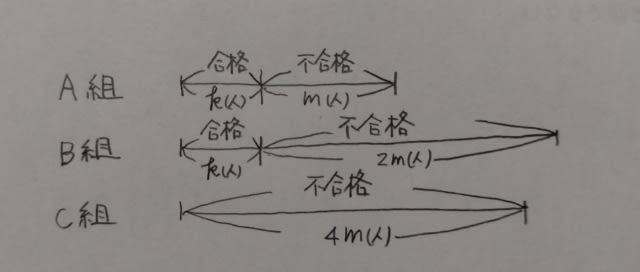
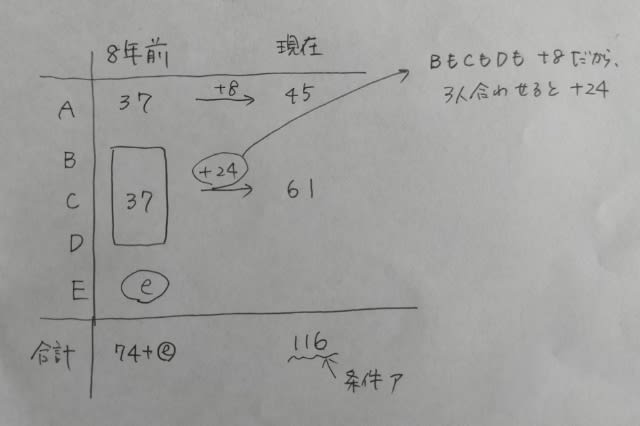
さて、2回目の試験では、A組の80%、B組の90%、C組全員が合格したので、2回目の試験が終わったにも関わらず、未だ合格できずに、もう学校なんかやめてやろうかと考えている人は、A組に0.2m人、B組にも0.2m人います。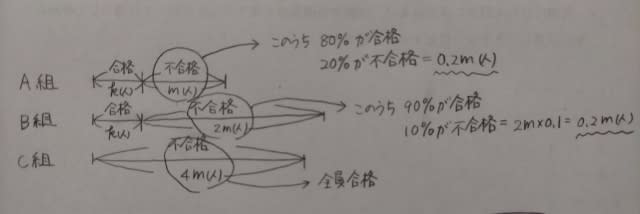
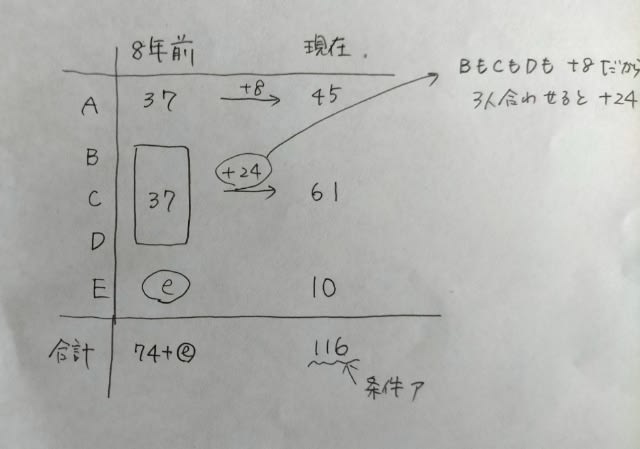
2回目の試験で不合格であった生徒は4人なので、0.2m+0.2m=4 という方程式ができます。これを解くと、m=10。よって、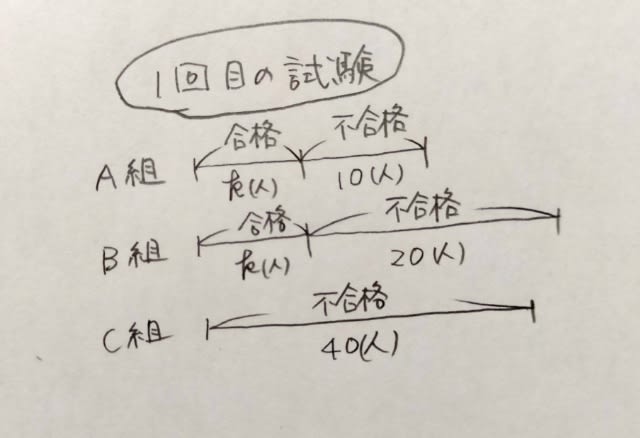
A、B、Cの3組で合計100人ですから、k+10+k+20+40=100 という方程式ができます。 これを解くとk=15。よってA組の生徒は25人。 それでは、正解を求めましょう。 A組で2回目の試験で合格した生徒は、10×0.8=8人。 8÷25×100=32。 正解は32%で、肢①です。ここをポチッとお願いします。→

1回目の試験では、A組とB組では同じ人数の生徒が合格し、不合格であった生徒の人数比はA組:B組:C組=1:2:4なので、

さて、2回目の試験では、A組の80%、B組の90%、C組全員が合格したので、2回目の試験が終わったにも関わらず、未だ合格できずに、もう学校なんかやめてやろうかと考えている人は、A組に0.2m人、B組にも0.2m人います。

2回目の試験で不合格であった生徒は4人なので、0.2m+0.2m=4 という方程式ができます。これを解くと、m=10。よって、

A、B、Cの3組で合計100人ですから、k+10+k+20+40=100 という方程式ができます。 これを解くとk=15。よってA組の生徒は25人。 それでは、正解を求めましょう。 A組で2回目の試験で合格した生徒は、10×0.8=8人。 8÷25×100=32。 正解は32%で、肢①です。ここをポチッとお願いします。→
にほんブログ村