関数y=xの2乗において、xの値がmからm+1まで増加するときの変化の割合が7になるとき、mの値として正しいものを、次の①〜⑤から1つ選べ。 ①3 ②4 ③7 ④8 ⑤15 関数において、変化の割合とは、「xが1だけ増加したときに、yの値がいくつ増加(減少)するか」のことで、
を計算して求めます。具体的には、こんな表を作ります。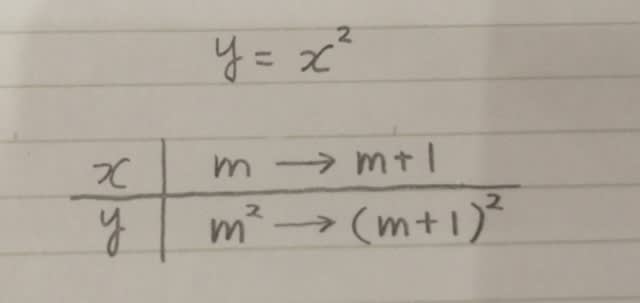
例えば、5→12であれば増加量は7ですね。その7は、12−5をして出てきた7です。m→m+1の場合は、(m+1)−m=1なので、xの増加量は1です。yの増加量は、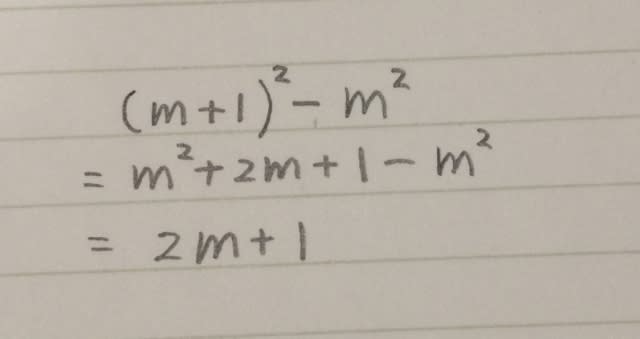
より、2m+1です。変化の割合が7だと問題に書いてあります。よって、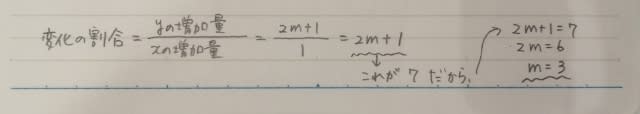
正解は、肢①です。また、y=ax2乗のときに限っては、こんなことになるので、覚えておいても損にはなりません。
ここをポチッとお願いします。→
にほんブログ村


を計算して求めます。具体的には、こんな表を作ります。
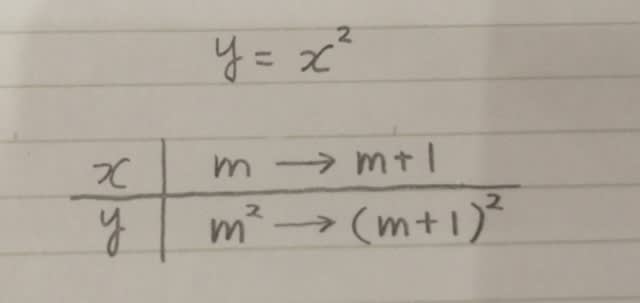
例えば、5→12であれば増加量は7ですね。その7は、12−5をして出てきた7です。m→m+1の場合は、(m+1)−m=1なので、xの増加量は1です。yの増加量は、
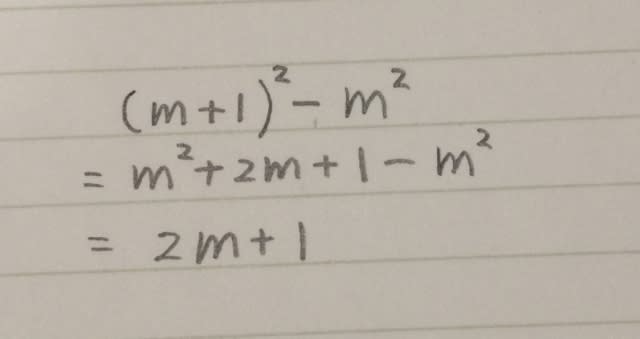
より、2m+1です。変化の割合が7だと問題に書いてあります。よって、
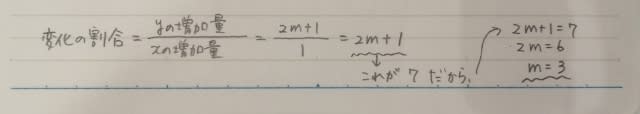
正解は、肢①です。また、y=ax2乗のときに限っては、こんなことになるので、覚えておいても損にはなりません。

ここをポチッとお願いします。→
にほんブログ村

























