A、B、C、Dの5人の年齢について、次のア〜オのことが分かっている。 ア.5人の現在の年齢の和は116である。 イ.DとCの現在の年齢を比べると、DはCよりも5歳年下である。 ウ.Bの現在の年齢を2倍すると、CとDの現在の年齢の和の3倍より3小さい。 エ.A、B、C、Dの8年前の年齢の和は74である。 オ.Aの8年前の年齢は、B、C、Dの8年前の年齢の和と等しい。 このとき、DとEの現在の年齢差はいくらか。①〜⑤から一つ選べ。ただし、現在も8年前も同じ日を基準とする。また、年齢はすべて整数値とする。 ①0歳差②1歳差③2歳差④3歳差⑤4歳差 エより、8年前には、A、B、C、D合わせて74歳でした。オより、8年前には、AはB、C、Dの和と等しかった。ってことは、Aは8年前には37歳だったということです。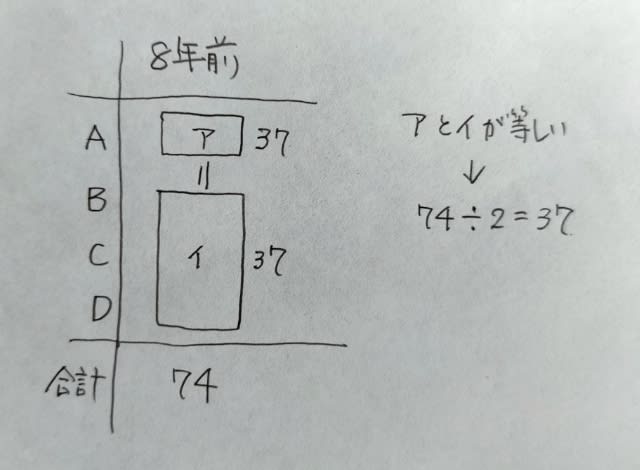
そこから8年経って現在です。8年経つと、誰でも8歳年を取ります。嫌だと言っても、お金を払うから許してくれといっても何をしても8歳年を取ります。だから、こうなってます。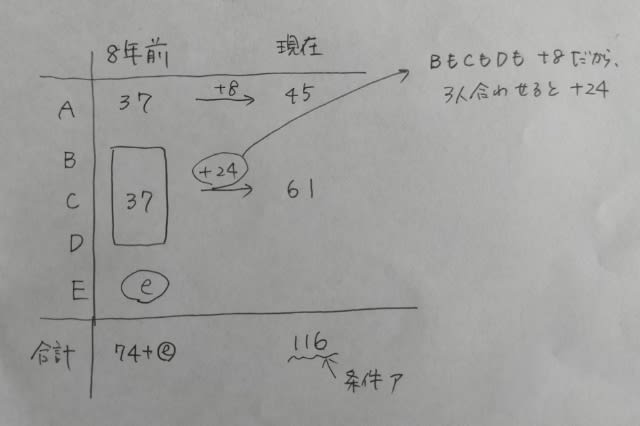
現在、Eは、116−45−61=10歳ですね。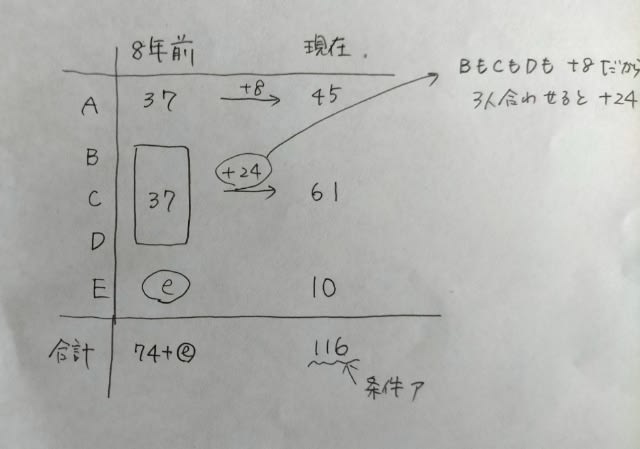
現在のB、C、Dの年齢を、それぞれb、c、dとすると、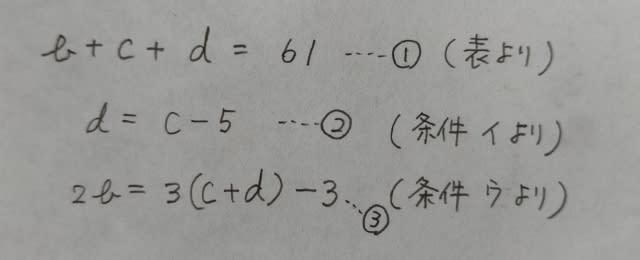
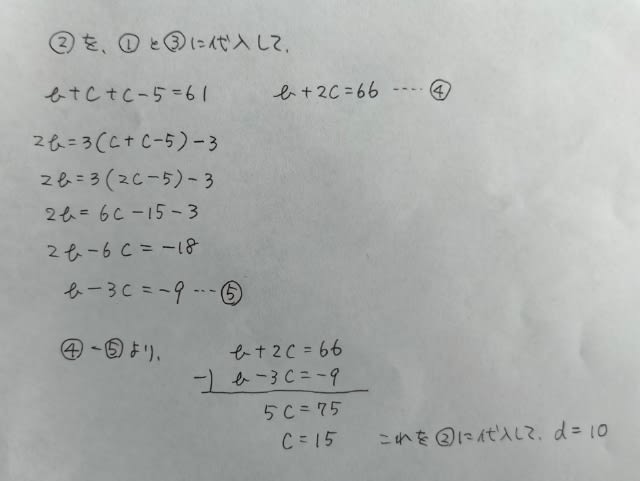
結局、DもEも10歳でした。正解は、肢①です。ここをポチッとお願いします。→

そこから8年経って現在です。8年経つと、誰でも8歳年を取ります。嫌だと言っても、お金を払うから許してくれといっても何をしても8歳年を取ります。だから、こうなってます。

現在、Eは、116−45−61=10歳ですね。

現在のB、C、Dの年齢を、それぞれb、c、dとすると、
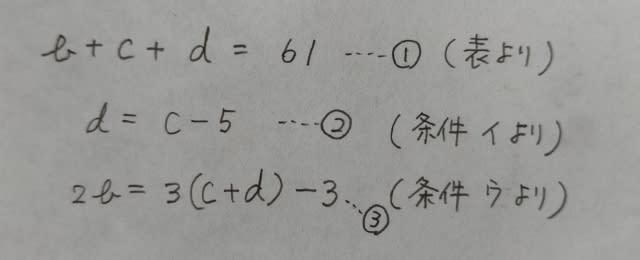
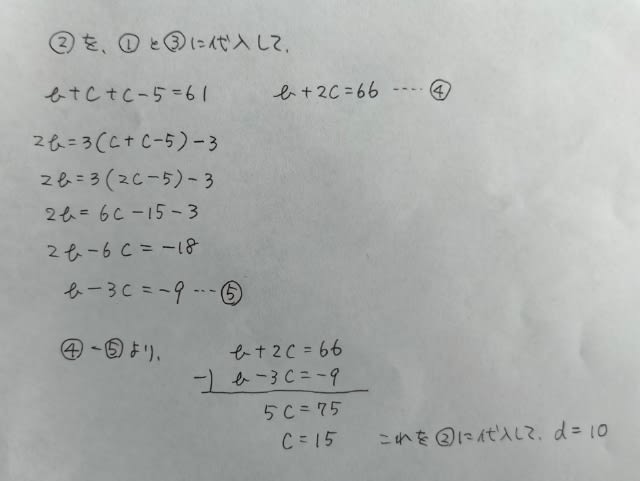
結局、DもEも10歳でした。正解は、肢①です。ここをポチッとお願いします。→
にほんブログ村