選べる学習メディア LECの通信講座
今年（平成29年）の国家一般職（大卒）の問題です。 A～Gの七つのバレーボールチームがある。Aは、B～Gの六つのチームと1試合ずつ対戦することになっているが、過去の対戦成績から、Bに勝つ確率は1／3であり、その他のチームに勝つ確率はいずれも1／2であることが分かっている。このとき、Aが4勝以上する確率はいくらか。 ただし、試合には引き分けはないものとする。 ①7／24②3／8③11／24④13／24⑤5／8 Aは、Bとの対戦のときだけ勝つ確率が違うので、場合分けをします。図にすると、
まず、Bに勝つ場合は、
Bに負ける場合は、画像のイとウのときだから、5／32＋1／32＝6／32。
よって、
正解は、肢①です。ここをポチッとお願いします。→
【どこよりもお得なauひかりサイトはここ！】
練習問題です。 1個のサイコロを何回か振って、奇数の目が3回出たところでやめるようにするとき、ちょうど6回振ったところでやめることになる確率を求めよ。 6回振って、3回奇数の目が出るから……と考えた人は失敗します。 例えば、はじめの3回で、3回とも奇数の目が出てしまったら、そこでやめてしまうからです。 「6回振ったところでやめることになる」とは、「6回目に3回目の奇数の目が出てやめることになる」という意味です。 つまり、1～5回目で奇数の目が2回出ていて、6回目を振ると奇数の目が出る。と考えるのですね。よって、
計算すると、
正解は、5／32です。 もう1問やってみて下さい。 サイコロを5回投げたとき、ちょうど5回目で2回目の1の目が出る確率を求めよ。（正解は、動物画像の下） 次回、国家一般職（大卒）の問題を紹介します。 ここをポチッとお願いします。→
正解125／1944
5肢択一の問題が3問あり、問題を読んでみたところ、サッパリ分からない。そこで、何も考えずに適当に答えた。このとき、2問正解する確率を求めてみます。 例えば、第1問と第2問が正解で、第3問が不正解であれば2問正解となりますので、
そんなこと言うんだったら、第1問と第3問が正解で、第2問が不正解でも2問正解じゃないか。
バカヤロー、第2問と第3問が正解で第1問が不正解でもいいじゃないか。
それ以外は2問正解にはならないなあ、などという議論になり、結局、
となります。 1／5は、正解する確率で、2問正解するから、2乗がくっついていて、4／5は、不正解の確率で、1問が不正解だから、1乗という訳なのですが、「3」は、なぜ「3」なのでしょうか？3問中2問正解が3パターンあるからです。では、なぜ3パターンなのかというと、3つの問題の中から、正解する2問を選ぶのが3通りあるからです。これは、
という意味ですね。まとめてみると、
以上のことから、反復試行の確率の公式ができるのです。 ♡何回やっても、確率が変わらないことを反復して行うときに、♤n回その試行をして、r回Aという事象が現れる確率は、
練習問題を次回やります。ここをポチッとお願いします。→
公式が使えない、くり抜きでもダメだったら、それは「延べ」の問題かも。例題です。 市役所採用試験から。 250人の学生が、英語、国語、および数学のテストを受けた。英語では110人、国語では120人、数学では112人が平均点以上であった。また、3科目すべてが平均点未満の者は50人、1科目だけ平均点以上だった者は94人であった。このとき、3科目すべてが平均点以上の者の数として正しいのは、次のうちどれか。①34人②36人③38人④40人⑤42人 平均点以上だった人は、英語110人、国語120人、数学112人だから、110＋120＋112＝342人。でも、テストを受けた者は250人。250人しかいないのに、何で342人もいるの？当然、ダブッている者があるからで、こういうときは、「延べ342人」と言うべきですね。 n（A）＋n（B）＋n（C）をすると、延べ人数が出ます。公式を考えたときのように、数えたところに✓をつけると、
仮に、3科目すべてが平均点以上の人が（実際に）10人いたとすると、延べにすると、10×3＝30人になってしまい、2科目だけ平均点以上の人が（実際に）30人いたとすると、延べにすると、30×2＝60人になります。3科目すべて平均点未満だった者は、何人いたとしても、延べには入りません。ということは、 ♤実際の人数も、延べ人数も分かっている。（本問の場合は、実際250人。延べ342人。）なおかつ、 ♡4つのグループ（3科目が平均点以上、2科目が平均点以上、1科目が平均点以上、0科目が平均点以上）のうち、2つ以上の人数が分かっている（本問の場合は、0科目50人、1科目94人）というときは、ベン図など描くことをせずに、いきなり、
正解は、肢②です。ベン図を描かなくてもよいので、助かりますね！ここをポチッとお願いします。→
うちは、マンション9階なのですが、玄関前に、かっこいい虫がいました。何という虫か分かりません。
公式が使えないとなると、真っ先に思い浮かぶのが、「くり抜き」という考え方です。例えば、
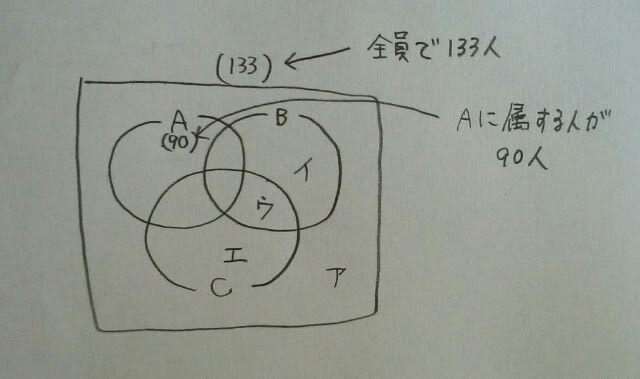全体の133人から、Aに属する90人をくり抜いて（引いて）しまえば、残りは43人です。つまり、ア＋イ＋ウ＋エ＝43。
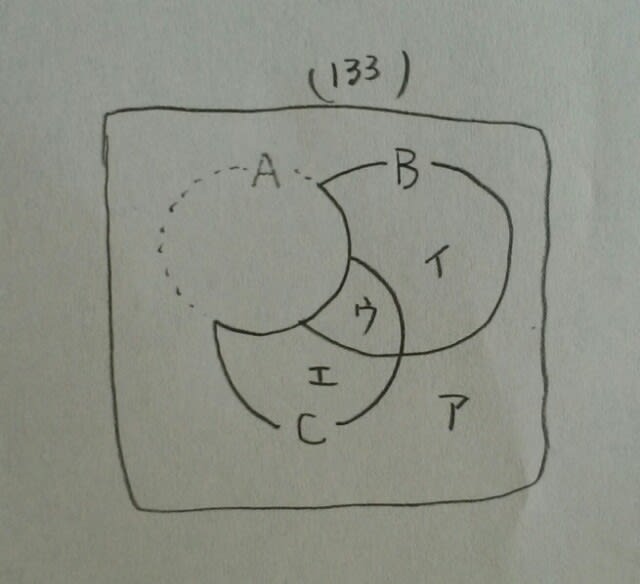例題です。A～Cの問題に生徒133人が取り組んだ。次のような結果が出たとき、確実に言えるのはどれか。 ・3問とも間違えた者は3人であった。 ・Aができた者は90人、AとBのみできた者は21人であった。 ・Bのみできた者はCのみできた者の2倍いて、Aのみできた者より8人多かった。 ・AとCのみできた者は16人で、BとCのみできた者より3人少なかった。 ①Aのみできた者は8人いる。 ②A、C両方できた者は66人いる。 ③A、C少なくともいずれか一つ正解した者は107人いる。 ④Bができた者は全部で101人いる。 ⑤Cができなかった者は52人いる。（平成27年大卒警察官） Cのみできた者がc人いたとすると、
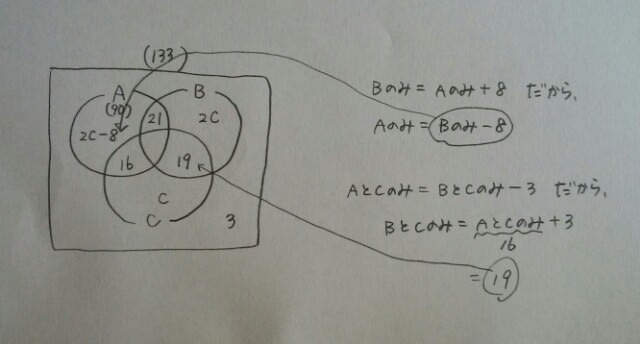Aをくり抜きますと、
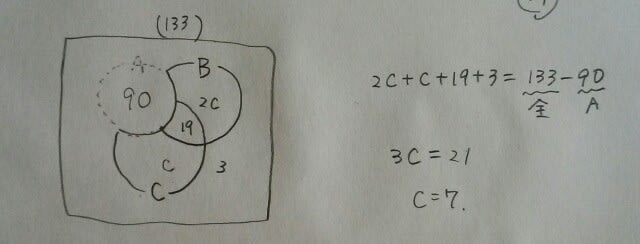元の図にc＝7を代入して、
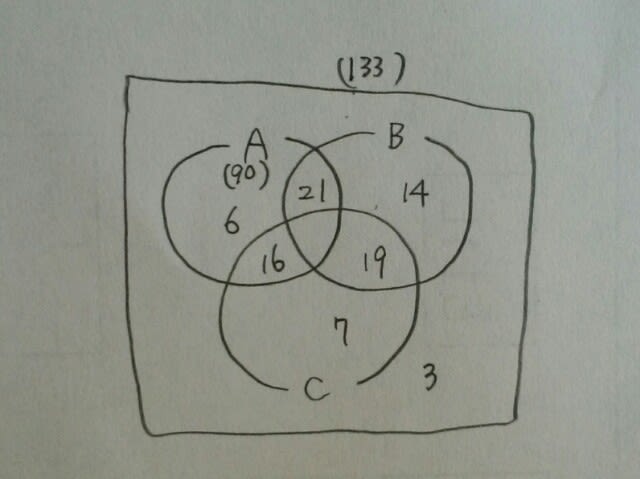3問とも正解した人は、90－21－6－16＝47人。
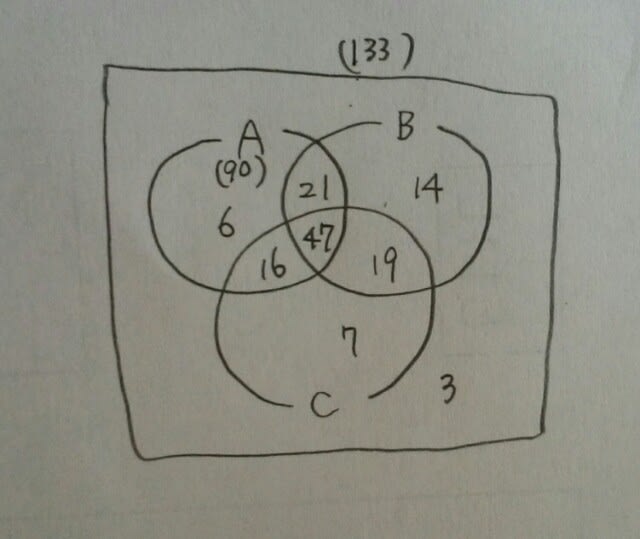肢①Aのみできた者は6人。 肢②A、C両方できた者は16＋47＝63人。 肢③A、C少なくともいずれか一つ正解した者は133－3－14＝116人。 肢④Bができた者は14＋21＋47＋19＝101人。 肢⑤Cができなかった者は133－6－21－14－3＝89人。 正解は、肢④です。 えっ？もう一つやってみたい？ページの下にカテゴリーがあるので、タップして下さい。「もっとみる」をタップ→集合をタップ→警視庁1類から（集合）平成25年9月21日という記事にありますよ。 公式も使えないし、くり抜きもできないときは、どうしたらいいんでしょうか？次へ続く。 ここをポチッとお願いします。→この前の台風後、京都鴨川がかなり増水していたとき。四条大橋から撮影。
