あるニ桁の正の整数aがある。158、204、273をaで割ると、いずれも割り切れず余りは等しくなる。このときaの各位の数の和はいくらか。 ①5 ②8 ③10 ④12 ⑤15 余りをxとおくと、
割られる数=割る数×商+余り なので、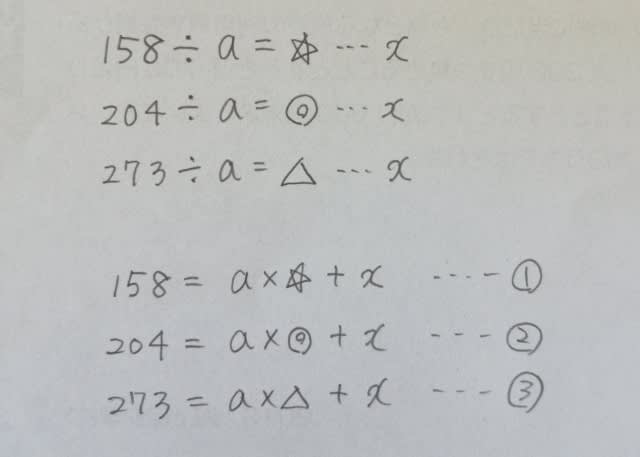
②から①を引けば、xが消えますね。
aに、(◎−☆)を掛けたものが46です。つまり、aは、46の約数なのです。 46の約数は、1、2、23、46です。aはニ桁と問題に書いてあります。よって、23か46です。 次に、③から①を引いてみましょう。別に③から②を引いたって構いませんよ。
aは115の約数です。115の約数は、1、5、23、115。このうち、ニ桁のものは23だけです。 ②−①から、aは23か46だと分かり、③−①から、aは23だとなりました。よって、a=23です。これは、教養試験問題てすから、これでOKです。 ただし、もしも、③−②をやってみたときに、a=23はあり得ないということになったらどうでしょうか?この問題自体が根底から覆されてしまいますね。こんなことは、時間の無駄かもしれませんが、念の為に確認してみましょう。
確かに、69の約数の中に、23は存在します。 間違いなくa=23です。 aの各位の数の和は2+3=5。正解は、肢①です。ここをポチッとお願いします。→

割られる数=割る数×商+余り なので、
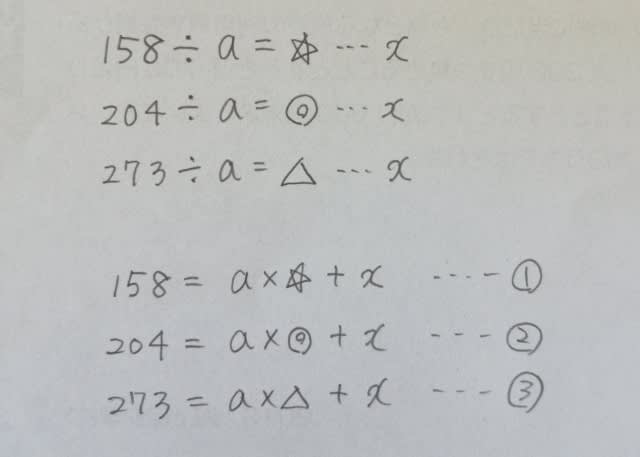
②から①を引けば、xが消えますね。

aに、(◎−☆)を掛けたものが46です。つまり、aは、46の約数なのです。 46の約数は、1、2、23、46です。aはニ桁と問題に書いてあります。よって、23か46です。 次に、③から①を引いてみましょう。別に③から②を引いたって構いませんよ。

aは115の約数です。115の約数は、1、5、23、115。このうち、ニ桁のものは23だけです。 ②−①から、aは23か46だと分かり、③−①から、aは23だとなりました。よって、a=23です。これは、教養試験問題てすから、これでOKです。 ただし、もしも、③−②をやってみたときに、a=23はあり得ないということになったらどうでしょうか?この問題自体が根底から覆されてしまいますね。こんなことは、時間の無駄かもしれませんが、念の為に確認してみましょう。

確かに、69の約数の中に、23は存在します。 間違いなくa=23です。 aの各位の数の和は2+3=5。正解は、肢①です。ここをポチッとお願いします。→
にほんブログ村













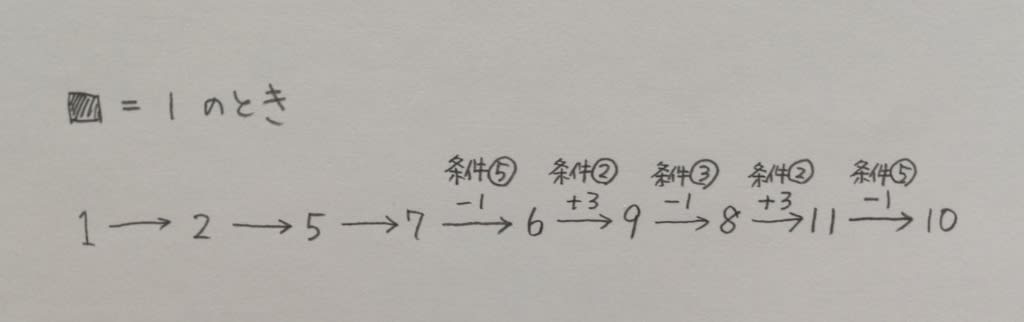

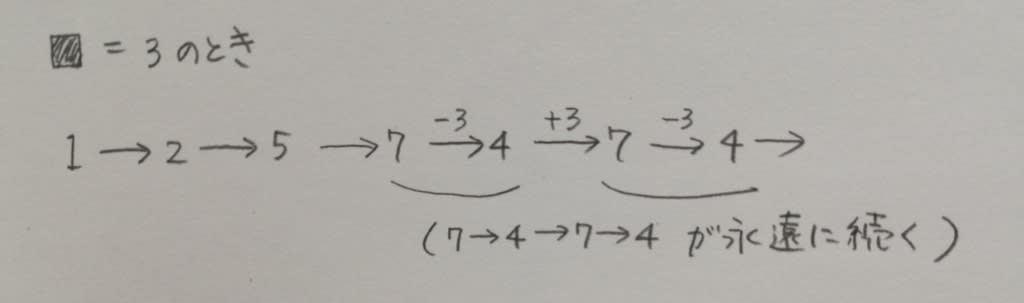





 だから、Aは22の約数、Bは3の倍数です。次に、
だから、Aは22の約数、Bは3の倍数です。次に、 だから、Aは6の倍数、Bは5の倍数です。よって、Aは22と6の公約数、つまり1か2です。
だから、Aは6の倍数、Bは5の倍数です。よって、Aは22と6の公約数、つまり1か2です。 しかし、Aが1ならば、B/Aは整数になってしまうので、結局Aは2しかありません。 Bは、3と5の公倍数、つまり15の倍数です。これは1つには決まりません。なので、いろいろ調べて、選択肢から選びます。
しかし、Aが1ならば、B/Aは整数になってしまうので、結局Aは2しかありません。 Bは、3と5の公倍数、つまり15の倍数です。これは1つには決まりません。なので、いろいろ調べて、選択肢から選びます。 一発目で見つかりました。正解は、肢②です。ここをポチッとお願いします。→
一発目で見つかりました。正解は、肢②です。ここをポチッとお願いします。→
