2019年度国家一般職(大卒)10

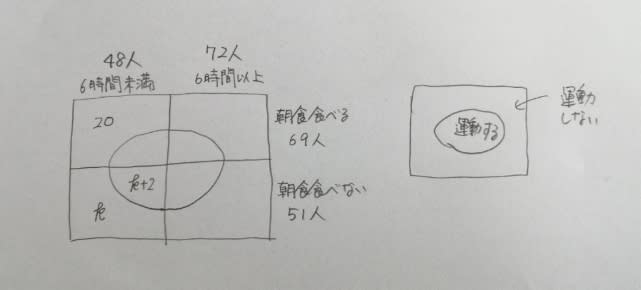
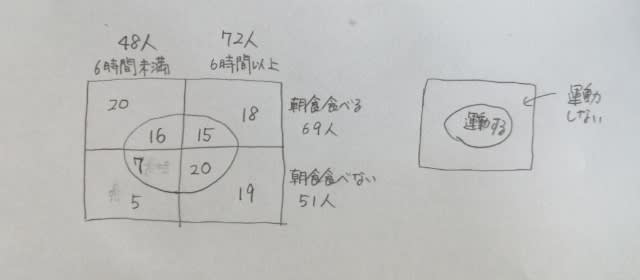
ある会社は、12月１日〜９日までの９日間について、トラック、バス、乗用車の各１台計３台の乗り物をA、Ｂ、Ｃの３社に貸し出すため、次の方針のとおり、計画を立てた。　　　　　　　　　　　　　　　　　　［方針］・いずれの乗り物も、１日単位で貸し出し、複数の日数を連続して貸し出してもよい。　　　　　　　　　　　　　　　　　　・いずれの乗り物も、各社間を移動する際には移動日を設け、AーC間は2日間、AーB間及びBーC間は1日とする。これらの移動日にはどの会社にも貸し出すことができない。　　　　　　　　　　　　　　　　　　・いずれの乗り物も、常に貸し出し日又は移動日となるよう貸し出し、Cには連続する2日間だけ貸し出す。　　　　　　　　　　　　　　　　　　・いずれの乗り物も、12月１日は全てAに貸し出し、6日は全てCに貸し出し、9日は全てBに貸し出す。また、4日はBに乗用車を、5日はCにバスを貸し出すのみとする。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12月1日〜6日までは計画どおり貸し出したが、6日にCが使用した後、乗り物のうち一つが故障したため、7日以降、その乗り物の貸し出しができなくなった。そこで、7日にCが使用する予定であった乗り物の一つについて、7日を移動日とし、8日から2日間Bに貸し出すよう変更したところ、全ての乗り物が2日間ずつBに貸し出されたことが分かった。このとき、確実にいえるのはどれか。　　　　　　　　　　　　　　　　　　①12月2日、バスは移動日であった。　　　　　　　　　　　　　　　　　　②12月3日、乗用車はBに貸し出された。　　　　　　　　　　　　　　　　　　③12月7日、トラックは計画どおりCに貸し出された。　　　　　　　　　　　　　　　　　　④12月8日、バスは計画では移動日であったが、Bに貸し出された。　　　　　　　　　　　　　　　　　　⑤12月8日、乗用車は計画どおり移動日であった。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　とりあえず、4つ目の方針。
3つ目の方針より、貸し出し日ではない日は、自動的に移動日になります。また、同じく3つ目の方針より、Cには連続する2日間だけ貸し出すので、7日のトラックと乗用車はCで、それ以外にCはありません。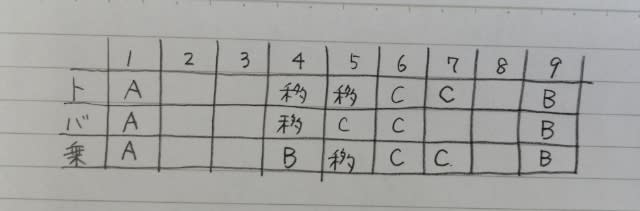
7日のバスは、移動日になり、どこに移動するかというと、2つ目の方針より、Bですよね。すると、8日のトラック、乗用車ともに移動日。

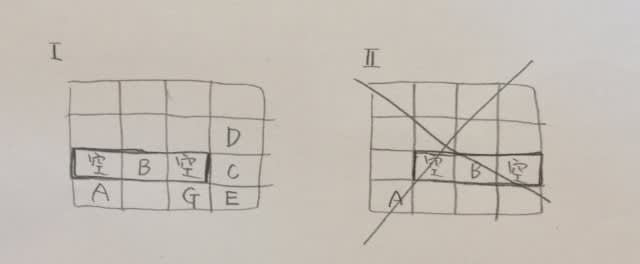
Cには、連続する2日間だけなので、1〜3日にはAかBか移動日しか入りません。さて、3日のトラックは、Aしかありません。(BだとするとBーCの移動が2日になるし、移動だとするとAーCの移動が3日以上になる)よって、トラックは1、2、3日連続でA。
6日に故障したのは何？最終的には、全ての乗り物が2日間ずつBに貸出されたのだから、それは乗用車です。
ということは、「7日にCが使用する予定であった乗り物の一つ」とは、トラックのことです。なので、
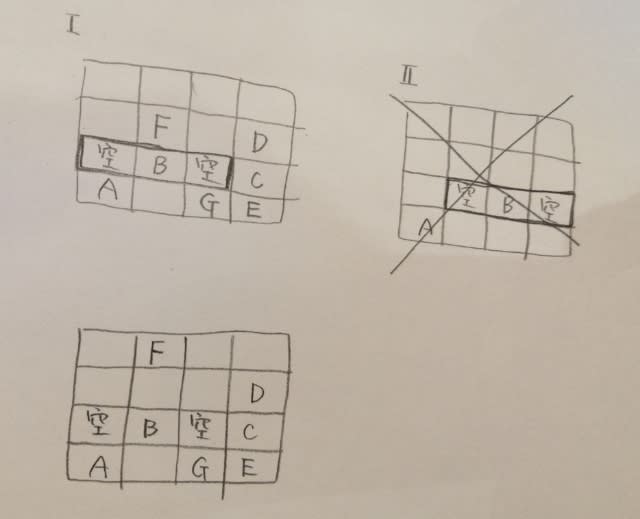
バスは8日と9日にBに貸し出されるので、AーCの移動が2日かかるのを考慮して、2日がA、3日が移動日。乗用車は2日間Bが使用するので、2日が移動日、3日がBです。
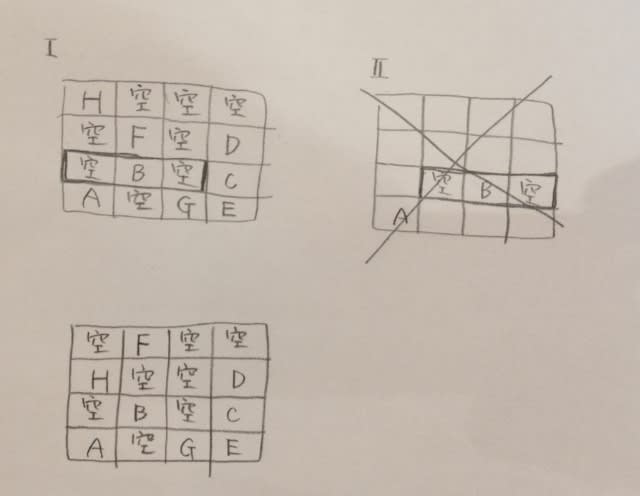
まとめると、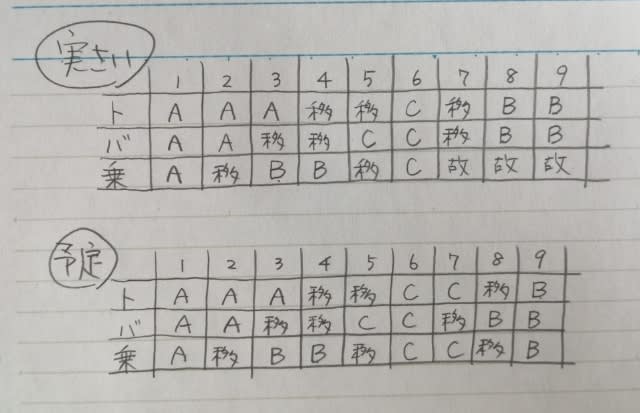
①2日、バスはAに貸し出された。②正解。③7日、確かにトラックはCに貸し出される予定だったが、移動日になってしまった。④8日、バスは計画ではBに貸し出される。⑤8日、乗用車は故障でアウト〜。　　　　　　　　　　　　　　　　　正解は、肢②です。ここをポチッとお願いします。→

にほんブログ村

2019年度国家一般職(大卒)9

図のような16の部屋から成る4階建てのワンルームマンションがある。　　　　　　　　　　　　　　　　　　A〜Hの8人がいずれかの部屋に1人ずつ住んでおり、A〜Hの8人が住んでいる部屋以外は空室である。　　　　　　　　　　　　　　　　　　また、各階とも東側から西側に向かって1号室、2号室、3号室、4号室の部屋番号である。　　　　　　　　　　　　　　　　　　このワンルームマンションについて次のことが分かっているとき、確実にいえるのはどれか。
○Aは1階の1号室に住んでいる。また、他の階で1号室に住んでいるのは、Hのみである。　　　　　　　　　　　　　　　　　○Bは2階に住んでいる。また、Bの隣の部屋は両方とも空室である。　　　　　　　　　　　　　　　　　○Cは、Dの一つ真下の部屋に住んでおり、かつEの一つ真上の部屋に住んでいる。また、Eの隣の部屋にはGが住んでいる。　　　　　　　　　　　　　　　　　○Fは2号室に住んでおり、Cより上の階に住んでいる。　　　　　　　　　　　　　　　　　○F、G、Hの3人はそれぞれ異なる階に住んでいる。　　　　　　　　　　　　　　　　　①BとCは異なる階に住んでいる。　　　　　　　　　　　　　　　　　②DとFは同じ階に住んでいる。　　　　　　　　　　　　　　　　　③Hの隣の部屋は空室である。　　　　　　　　　　　　　　　　　④1階に住んでいるのは2人である。　　　　　　　　　　　　　　　　　⑤全ての部屋が空室である階がある。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　条件を整理すると、こんな感じです。
このワンルームマンションは4階建て。㋑を見ると、EとGは、1階か2階に住んでいます。　　　　　　　　　　　　　　　　　　　でもでも、2階に住んでいるとすると、㋐と合わせて考えると、2階には5部屋以上あることになります。ゆえに、EとGは1階です。
あとは、もう何だか分からないので、とりあえず、㋐を使って、場合分けしましょう。
Ⅱは、㋑が入りません。よってⅠです。Ⅰに㋑を入れます。
Fは、Cより上で2号室だから、3階の2号室か、4階の2号室。
㋒より、Fが3階ならHは4階。Fが4階ならHは3階。(Hは1号室)
こんなに空室だらけで、マンション経営大丈夫なの?①BとCは同じ階。②同じ階かもしれないが、異なる階かもしれない。③正解。④1階は3人。⑤そんな階はない。正解は、肢③です。ここをポチッとお願いします。→

にほんブログ村

教員採用試験教養数学の鉄板問題その2(素数)

素数とは、1とその数自身しか約数を持たない(割り切ることができない)数のことで、1は除きます(1は素数ではありません)。　　　　　　　　　　　　　　　　　　それがどうしたと言われると困ってしまうのですが、これが数学の世界では大変重要かつ興味深いもので、なんともかんともえらいことになっていくのですが、そんなに難しい問題が教養数学で出題はされませんので、とりあえず覚えて下さい。　　　　　　　　　　　　　　　　　　　例えば、「20までの自然数のな中に含まれる素数は全部で何個あるか?」などと出題されています。　　　　　　　　　　　　　　　　　　一番小さい素数は2ですね。次は3、次は5、次は7、次は11、次は13、次は17、次は19。だから正解は8個です。　　　　　　　　　　　　　　　　　　この8個は、覚えてしまってもいいでしょう。2、3、5、7ですから、「ふみ(文)こない」などと。あとの4つの覚え方は知りません。　　　　　　　　　　　　　　　　　　　　でも、「50 までの自然数の中にに含まれる素数を全て足すといくらか？」などという鬼👹問題が出たらどうしましょう?実際にあったと思います。　　　　　　　　　　　　　　　　　　普段数学に親しんでいる者ならば、普通にやれますが、慣れていない人にとってはまさに👹問題ですね。　　　　　　　　　　　　　　　　　　「エラトステネスのふるい」というものがあります。まず、1から50まで順番に数字を並べます。
1は、素数ではありませんから、1を消します。
その隣の2が素数です。なので2を○で囲みます。
今○で囲んだ2の倍数は、もはや素数ではないので、全て消します。　　　　　　　　　　　　　　　　　　○で囲んだ2の隣の3が素数です。なので3を○で囲みます。
○で囲んだ3の倍数は、もはや素数ではないので、消します。もう消えている6などは、わざわざもう一度消す必要はありません。ほっといて下さい。
この作業を、8以下まで繰り返せば出来上がりです。(なぜ8かは後述。えっ？最後までやれって?はいはい、承知しました。5を○で囲みます。
5の倍数を消しまして〜。
7を○で囲んで〜。
7の倍数消して〜。
すると、もう8は消えているので、残っているものを全て○で囲みます。
こいつらが50以下の素数です。ゆえにその和は、328です。　　　　　　　　　　　　　　　　　　ところで、なぜ8までやるのかというと、ルート50は7より大きくて8より小さいからです。　　　　　　　　　　　　　　　　　　1から1000の範囲で素数を全て見つけたければ(そんな人はいないと思うのですが)、ルート1000は31と32の間ですから、(31×31＝961、32×32＝1024)32がくるまでこの地味な作業を繰り返せばよいのです。　　　　　　　　　　　　　　　　　　1から1000まで書くのが一番辛い作業です。ここをポチッとするのは簡単な作業です。→
にほんブログ村

2019年度国家一般職(大卒)8

ある会社で社員の生活習慣について調査を行った。次のことが分かっているとき、確実にいえるのはどれか。　　　　　　　　　　　　　　　　　　○睡眠時間の平均が6時間以上の者は72人であり、6時間未満の者は48人である。　　　　　　　　　　　　　　　　　　○朝食を食べる習慣がない者は51人である。　　　　　　　　　　　　　　　　　　○朝食を食べる習慣があり、運動する習慣がなく、睡眠時間の平均が6時間未満の者は20人である。　　　　　　　　　　　　　　　　　　○朝食を食べる習慣がなく、睡眠時間の平均が6時間未満の者のうち、運動する習慣がある者は、そうでない者より2人多い。　　　　　　　　　　　　　　　　　　○運動する習慣がなく、睡眠時間の平均が6時間未満の者は25人である。　　　　　　　　　　　　　　　　　　○運動する習慣があり、睡眠時間の平均が6時間以上の者のうち、朝食を食べる習慣がある者は15人であり、そうでない者より5人少ない。　　　　　　　　　　　　　　　　　　①運動する習慣がある者は55人である。　　　　　　　　　　　　　　　　　　②睡眠時間の平均が6時間以上で、朝食を食べる習慣があり、運動する習慣がない者は15人である。　　　　　　　　　　　　　　　　　　③睡眠時間の平均が6時間未満で、朝食を食べる習慣があり、運動する習慣がある者は20人である。　　　　　　　　　　　　　　　　　　④睡眠時間の平均が6時間以上の者のうち、朝食を食べる習慣がある者は、そうでない者より少ない。　　　　　　　　　　　　　　　　　　⑤朝食を食べる習慣がない者のうち、運動する習慣がある者は、そうでない者より少ない。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　キャロル図を使う問題ですね。1〜4番目までの条件を書き込むと、
(はじめの条件から、全体で120人。4番目の条件の、そうでない者をk人としています。)　　　　　　　　　　　　　　　　　　ここで、5番目の条件を見ると、ラッキー、ポッキー、k＝5だと分かりますので、
睡眠時間が6時間未満の列(左列)の合計は48人だから、
最後の条件を書き込んで、
空いている場所は、引き算すれば人数が分かります。
選択肢①58人。②18人。③16人。④確かに少ない。⑤多い。正解は肢④です。　　　　　　　　　　　　　　　　　　　　　　ここをポチッとお願いします。→
にほんブログ村

教員採用試験教養数学の鉄板問題その1(四則計算)

単なる加減乗除の計算ですが、よく出題されます。　　　　　　　　　　　　　　　　　　例えば、2019年度の神奈川県。正誤判定ですが、
実際は、これを計算すると20であるというのが正しいか誤りかを判定する問題です。　　　　　　　　　　　　　　　　　我々、小学生のとき、かっこがあれば、かっこの中を先に計算し、掛け算や割り算は、足し算や引き算よりも先に計算するべしと習ったわけですが、中学になると、指数が登場するので、結局、①指数②かっこ③乗除④加減の順に計算するということになりましたね。よって、こうなります。
ところで、計算問題をたくさん解いていると、0.25や0.75という小数がしょっちゅう出てきますね。　　　　　　　　　　　　　　　　　はじめのうちは、0.25は100分の25で、これを約分していくと4分の1になって、などとやるのですが、いつか、0.25は4分の1、0.75は4分の3だと覚えてしまいます。　　　　　　　　　　　　　　　　　もっと慣れてくると、0.125が8分の1、0.375が8分の3、0.625が8分の5、0.875が8分の7も覚えてしまい、3.5なども、7の半分だから、2分の7とできるようになります。　同じく2019年度愛媛県では、こうです。
やってみます。
け、計算ドリルやるべき?ここをポチッとお願いします。→
にほんブログ村