平行四辺形には、4つの性質があります。①2組の対辺が平行である。②2組の対辺の長さが等しい。③2組の対角が等しい。④対角線が、それぞれの中点で交わる。
そして、平行四辺形になる条件が5つあります。その5つのうちの1つでもあてはまっていれば、その四角形は、平行四辺形です。その5つとは、性質の①～④と、⑤1組の対辺が、平行で、かつ長さが等しいです。
では、前回の最終図です。
∠O1HI＝∠O2IH＝90ºなので、O1H∥O2I。かつ、O1H＝O2I。平行四辺形になる条件の⑤にあてはまっていますので、四角形O1HIO2は平行四辺形です。しかも、∠O1HI＝∠O2IH＝90ºなのですから、もうこれはなんと言ったって長方形です。よって、
この図に見覚えはありませんか？前編の始めにやった、ウォーミングアップの図なのです。
このrは、8でした。前編と後編に渡っていますので、おさらいをしますと、2017年度の国家一般職（大卒）。 図のように、円A、B、Cと直線lが互いに接している。円Aと円Bの半径が等しく、また、円Cの半径が2であるとき、円Aの半径はいくらか。
①4√3②7③8④6√2⑤9 の正解は、肢③ということです。 ここをポチッとお願いします。→
にほんブログ村
まず、ウォーミングアップから。rの値を求めて下さい。
三平方の定理が使えそうですね。DからABに垂線を下ろします。
四角形HBCDは、3つの角が直角なので、もう一つの角も直角になり、長方形です。ゆえにHD＝r。HB＝2だから、AH＝r－2。
図形には、3つの手筋があります。 ①線対称なものには、軸を入れる。 ②円と接線があれば、円の中心と接点を結ぶ（結んだ線と接線は90º） ③円と円、球と球が接していたら、中心どうしを結ぶ。 図にしてみると、
②は、①とほとんど同じことなので、2つの手筋といっても構いません。 接弦定理を使ったりするときには、②の線はじゃまになったりするときもありますが、まあ、必ずといっていいほど、こういう手筋は使います。 例えば、2017年度の国家一般職（大卒）。 図のように、円A、B、Cと直線lが互いに接している。円Aと円Bの半径が等しく、また、円Cの半径が2であるとき、円Aの半径はいくらか。
①4√3②7③8④6√2⑤9 なぜ斜めにしてあるのでしょうか？この問題を、少しでも難しく感じさせるためです。まっすぐにしますと……
ほんの少しだけ、右側の円が大きく見えるのは、目の錯覚でしょうか？とりあえず線対称なので、軸をひきます。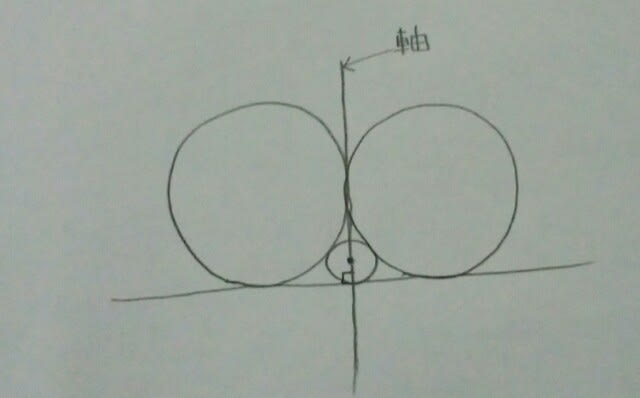
小さい円の中心は、必ず軸上にあります。もしなかったとしたら、円の中心が2箇所あることになるからです。
手筋②と③もやりますと、
ここで、四角形O1HIO2は、長方形です。何も、バカ丁寧に証明などする必要はないのですが、ここは勉強のために、少し回り道をしてみましょう。四角形O1HIO2が長方形であることを証明してみて下さい。ここをポチッとお願いします。→
図Ⅰの円周上にA～Fの6点が等間隔に並んでいる。これらの点から、図Ⅱのように任意に3点を選び、三角形を作る。このとき、作られる三角形のうち、正三角形、直角三角形の個数の組合せとして、最も妥当なのはどれか。
点を、1つおきに結ぶと、正三角形ができます。
そして、これ以上正三角形を作ることはできません。正三角形は2個。円の直径があれば、
円周角は、全て90ºです。
図Ⅱの場合、ADが直径です。したがって、
同様に、BEを直径としたときも4つ。CFを直径としたときも4つ。合計12個できます。よって、正解は、肢②です。
