LECオンラインショップ(E学習センター)


 1. 2<√a<3を満たす正の整数aは何個あるか。 ア.4個 イ.5個 ウ.6個 エ.7個 オ.8個 2乗して考える方法と、ルートのまま考える方法の2つあります。 ①2乗して考える。 2<√a<3ということは、正の範囲に限られるので、すべて2乗して、4<a<9。これを満たすaは、5、6、7、8の4個なので、正解はアです。 ②ルートのまま考える。 2=√4、3=√9だから、√4<√a<√9。これを満たすaは、5、6、7、8の4個。 まあ、①も②も同じことなんですけどね。 2
1. 2<√a<3を満たす正の整数aは何個あるか。 ア.4個 イ.5個 ウ.6個 エ.7個 オ.8個 2乗して考える方法と、ルートのまま考える方法の2つあります。 ①2乗して考える。 2<√a<3ということは、正の範囲に限られるので、すべて2乗して、4<a<9。これを満たすaは、5、6、7、8の4個なので、正解はアです。 ②ルートのまま考える。 2=√4、3=√9だから、√4<√a<√9。これを満たすaは、5、6、7、8の4個。 まあ、①も②も同じことなんですけどね。 2 選択肢のアが5なので、nに5を代入すると、25-20-5=0。0は、素数ではないのでダメ。ってな具合で、調べれば簡単です。 選択肢がなければ、こうします。あっ、まずは素数ですよね。1と、その数自身しか約数をもたないものを素数といいます。ただし、1は素数ではありません。
選択肢のアが5なので、nに5を代入すると、25-20-5=0。0は、素数ではないのでダメ。ってな具合で、調べれば簡単です。 選択肢がなければ、こうします。あっ、まずは素数ですよね。1と、その数自身しか約数をもたないものを素数といいます。ただし、1は素数ではありません。 nは、正の整数なので、(n-5)と、(n+1)とでは、必ず(n-5)の方が小さい。素数は、素因数分解すると、1×その数となるのだから、n-5=1で、n+1=その数です。よって、n=6。その数=7です。正解は肢イです。
nは、正の整数なので、(n-5)と、(n+1)とでは、必ず(n-5)の方が小さい。素数は、素因数分解すると、1×その数となるのだから、n-5=1で、n+1=その数です。よって、n=6。その数=7です。正解は肢イです。



 選択肢のアが5なので、nに5を代入すると、25-20-5=0。0は、素数ではないのでダメ。ってな具合で、調べれば簡単です。 選択肢がなければ、こうします。あっ、まずは素数ですよね。1と、その数自身しか約数をもたないものを素数といいます。ただし、1は素数ではありません。
選択肢のアが5なので、nに5を代入すると、25-20-5=0。0は、素数ではないのでダメ。ってな具合で、調べれば簡単です。 選択肢がなければ、こうします。あっ、まずは素数ですよね。1と、その数自身しか約数をもたないものを素数といいます。ただし、1は素数ではありません。 nは、正の整数なので、(n-5)と、(n+1)とでは、必ず(n-5)の方が小さい。素数は、素因数分解すると、1×その数となるのだから、n-5=1で、n+1=その数です。よって、n=6。その数=7です。正解は肢イです。
nは、正の整数なので、(n-5)と、(n+1)とでは、必ず(n-5)の方が小さい。素数は、素因数分解すると、1×その数となるのだから、n-5=1で、n+1=その数です。よって、n=6。その数=7です。正解は肢イです。











 のとき、P(A)+P(B)の値として、最も妥当なのはどれか。
のとき、P(A)+P(B)の値として、最も妥当なのはどれか。 ∪(または)、∩(かつ)ですね。
∪(または)、∩(かつ)ですね。
 は、AまたはBではない部分。AまたはBが、アとイとウですから、アとイとウ以外の部分、つまりエを表しています。よって、エ=0.2です。次に、
は、AまたはBではない部分。AまたはBが、アとイとウですから、アとイとウ以外の部分、つまりエを表しています。よって、エ=0.2です。次に、 は、Aではない(ウとエ)またはBではない(アとエ)ですから、アとウとエを表しています。つまり、ア+ウ+エ=0.9。よって、
は、Aではない(ウとエ)またはBではない(アとエ)ですから、アとウとエを表しています。つまり、ア+ウ+エ=0.9。よって、 正解は、肢⑤です。
正解は、肢⑤です。

 対数、複利計算について知らない人は、前回の記事を見てから戻ってきて下さいね。おっと、前回logについて説明しましたが、一つ説明するのを忘れていました。logの計算の公式をいろいろ紹介しましたが、そもそもlogを使うにあたって、大前提となる事柄があります。それは、
対数、複利計算について知らない人は、前回の記事を見てから戻ってきて下さいね。おっと、前回logについて説明しましたが、一つ説明するのを忘れていました。logの計算の公式をいろいろ紹介しましたが、そもそもlogを使うにあたって、大前提となる事柄があります。それは、 ということです。赤で線を引っ張った条件にあてはまらないときは、計算もできませんし、logを使った議論は成り立ちません。記述式の数学では、この条件を書き忘れて減点ということがよくありますが、公務員試験では、ほとんど気にしなくても構いません。(絶対とは言えませんが)さて、本問について。「年利率」と書いてあるので、利子は1年に1回。x年経つと、利子はx回つきます。前回の、複利計算の公式より、x年後には、
ということです。赤で線を引っ張った条件にあてはまらないときは、計算もできませんし、logを使った議論は成り立ちません。記述式の数学では、この条件を書き忘れて減点ということがよくありますが、公務員試験では、ほとんど気にしなくても構いません。(絶対とは言えませんが)さて、本問について。「年利率」と書いてあるので、利子は1年に1回。x年経つと、利子はx回つきます。前回の、複利計算の公式より、x年後には、
 ここから、はじめて対数をやる人にとっては、信じられないことをします。知ってる人は知ってますよね。そう、「常用対数をとる」のです。
ここから、はじめて対数をやる人にとっては、信じられないことをします。知ってる人は知ってますよね。そう、「常用対数をとる」のです。 よって、正解は肢③です。おいおい、待ってくれって?結構しんどい計算ですね。そこで抜け道。っていうか、むしろこっちの方が本筋かも。
よって、正解は肢③です。おいおい、待ってくれって?結構しんどい計算ですね。そこで抜け道。っていうか、むしろこっちの方が本筋かも。 まあ、資料解釈のつもりで、ひたすら筆算。
まあ、資料解釈のつもりで、ひたすら筆算。

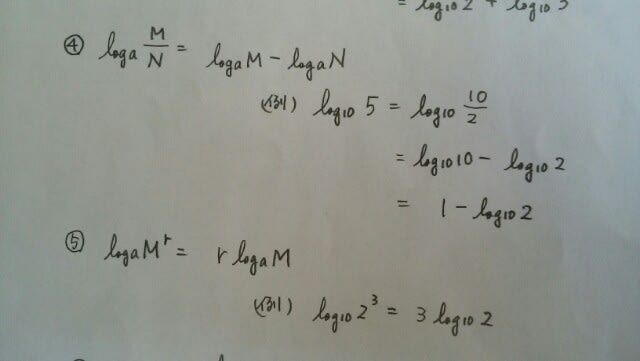
 といったところです。えっ?ややこしい?ちょっと慣れていただきましょう。次の計算をやってみてください。
といったところです。えっ?ややこしい?ちょっと慣れていただきましょう。次の計算をやってみてください。 答えは、
答えは、
 途中の計算過程は、あくまでも一例であって、他にもいろいろあります。最後の数字と一致していれば正解です。もう少し練習したい人は、最後に載せるやつをやって、慣れて下さい。ただ、次回言いますが、根性で何とかすることもできますので、理解するのがどうしても無理なら、ほっといてもいいでしょう。次に、複利計算の公式です。利率A%(複利)で、N回利子がかかると、次のようになります。
途中の計算過程は、あくまでも一例であって、他にもいろいろあります。最後の数字と一致していれば正解です。もう少し練習したい人は、最後に載せるやつをやって、慣れて下さい。ただ、次回言いますが、根性で何とかすることもできますので、理解するのがどうしても無理なら、ほっといてもいいでしょう。次に、複利計算の公式です。利率A%(複利)で、N回利子がかかると、次のようになります。 何?これも難しい?ちょっと練習しましょう。例えば、今200万円を年利率10%の複利で運用を始めたら、3年後はどうなる?
何?これも難しい?ちょっと練習しましょう。例えば、今200万円を年利率10%の複利で運用を始めたら、3年後はどうなる? もう一丁!100万円を、半年複利20%で2年運用すると?
もう一丁!100万円を、半年複利20%で2年運用すると? はい、お疲れさまでした。それでは、対数の計算問題です。
はい、お疲れさまでした。それでは、対数の計算問題です。


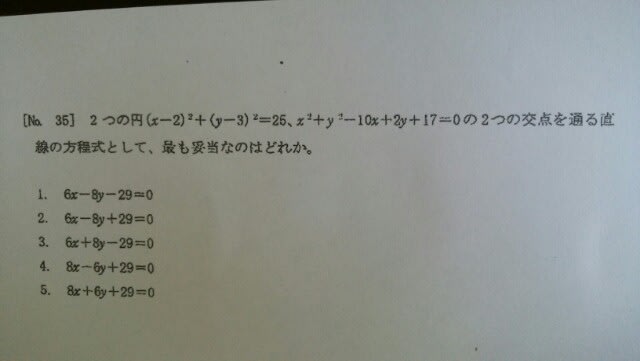 円について、よく知らない場合は、この1つ前の記事をご覧下さいね。さて、円の方程式の基礎(中心の座標や、半径)を知っているだけでは、この問題は解けませんね。選択肢も使えそうにありません。この場合は、次の有名な公式を覚えておかなければいけないのです。
円について、よく知らない場合は、この1つ前の記事をご覧下さいね。さて、円の方程式の基礎(中心の座標や、半径)を知っているだけでは、この問題は解けませんね。選択肢も使えそうにありません。この場合は、次の有名な公式を覚えておかなければいけないのです。 本問の場合は、
本問の場合は、 よって、正解は、肢①です。えっ、円①と円②を逆にしてもダイジョウブかって?もちろんダイジョウブですよ。
よって、正解は、肢①です。えっ、円①と円②を逆にしてもダイジョウブかって?もちろんダイジョウブですよ。 ほらね。しかしながら、これで納得してしまった人は、実はよくないのです。もう一度、公式をよく読んでね。「異なる2点で交わるとき」って書いてあるでしょ。これが、記述式のテストだったら、この2円が、異なる2点で交わることを、きちんと示さなければいけないのですが、選択肢から選ぶ場合は、「交わるから問題に出してるんでしょうが」と、勝手に進めてしまいましょう。では、練習問題です。これも、勝手に、異なる2点で交わるものと決めつけてやって下さいね。
ほらね。しかしながら、これで納得してしまった人は、実はよくないのです。もう一度、公式をよく読んでね。「異なる2点で交わるとき」って書いてあるでしょ。これが、記述式のテストだったら、この2円が、異なる2点で交わることを、きちんと示さなければいけないのですが、選択肢から選ぶ場合は、「交わるから問題に出してるんでしょうが」と、勝手に進めてしまいましょう。では、練習問題です。これも、勝手に、異なる2点で交わるものと決めつけてやって下さいね。

