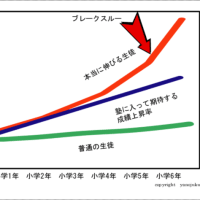
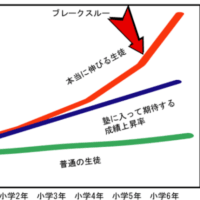
実は中学までの勉強というのは
才能は全く要りません。特に数学や理科において、
小学校の学習内容をきっちりと身につけていれば、
中学3年間の数学や理科は基礎・応用をきっちり学習すれば、
かならず習得は可能です。
しかし、しかしです。
高校数学はやはり数学的センスが必要です。
どう頑張っても、文系型の人は理系的な数学的センスの持ち主には
かなわないのです。
数学オリンピックの問題をみてみてください。
ああいった問題は過去のパタン的に記憶した数学力では
まったく歯がたたないのです。
数学的センスを持った人は数学の問題を解くときに
数学の公式なんかは使いません。
むしろ公式を自分で考え出してしまうような感性で、問題を解いていきます。
それは生まれ持った天性で、誰かの指導によって
導かれるものではないのです。
理系の上位者にはそういう人がゴロゴロいます。
数学の模試の上位者とは、まさにそういう人たちです。
数学の苦手な人は、最初はわかりませんが、
高校の数学の単元の多さにびっくりするでしょう。
確率・数列・ベクトル・統計・集合
さらに関数系では三角比/三角関数や
二次間数三次関数や三角関数
指数・対数、微積。
それを二年ほどで習得しないといけないのです。
計算力ももちろん必要としますが、論理的な流れを考えることが
好きでないと、とてもこれらの単元を修得するのは
むずかしいでしょう。
大量に問題を解けばいいのでしょと闇雲に問題を解いても
それは時間を浪費するばかりです。
模試の数学のテストで同じ問題は殆ど出ないのです。
もともと数学の得意でない人は
ミスが多いです。正解に辿り着くまでに
ミス連発ですっかりやる気を無くしてしまうのです。
まさに、ランニング中にこけてばかりで、
怪我をして、ゴールの前でうなだれている
長距離ランナーのようなものです。
数学の先生は数学を解くのが得意なので、
学校の授業でもそうですが、解けない生徒の気持ちが
わかりません。
本当はそれではいけないのでしょうが、
できない人の気持ちがわからないのです。
一番大切なことは、理解できないことを
丸暗記にしないことです。
とにかく公式でも何でもまずは
その成り立ちから考える、自分から公式の成り立ちに
関わっていけば、けっこう公式は頭に残ります。