毎日いろんなことで頭を悩ましながらも、明日のために頑張ろうと自分を励ましています。
疲れるけど、頑張ろう!
カレンダー
| 2022年2月 | ||||||||
| 日 | 月 | 火 | 水 | 木 | 金 | 土 | ||
| 1 | 2 | 3 | 4 | 5 | ||||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | ||
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | ||
| 27 | 28 | |||||||
|
||||||||
goo ブログ
過去の記事
カテゴリ
| 藤井聡太(519) |
| 松井・マー君(166) |
| 読書(251) |
| 映画・DVD(124) |
| 家族(271) |
| 塾(267) |
| 思うこと(296) |
| 日々の暮らし(638) |
| 時事(278) |
| お出かけ(279) |
| おいしいもの(274) |
| PC・ブログ(155) |
| コレクション・LEGO(594) |
| お友だち(41) |
| お遊び・実験・工作(90) |
| 思ひ出(24) |
| 動・植物・自然(521) |
| SMAP・藤原・小栗(89) |
| からだ(140) |
| スポーツ(164) |
| テレビ(76) |
| 音楽(88) |
| わが街(158) |
| 失敗・醜態(51) |
| 事件(32) |
| マンガ・アニメ(33) |
| 甥っ子・姪っ子(29) |
| お話(23) |
| 美術(30) |
| 車(71) |
| 特技・自慢(36) |
最新の投稿
最新のコメント
| 塾長/「世界の終わりとハードボイルド・ワンダーランド」 |
| kumanomi/「世界の終わりとハードボイルド・ワンダーランド」 |
| 三文字(i e π)寄れば文殊のヒフミヨ/「だんご3兄弟」 |
| ぴよ/名前は? |
| ウィッシュ好き/六月の子守唄 |
| あみ/巨大セロームのなれの果て |
| 塾長/LEGO 10303 余談 |
| ようき/LEGO 10303 余談 |
| 呑んだくれブルース/「空中ブランコ」 |
| 塾長/ジャングル部屋 |
最新のトラックバック
ブックマーク
|
豚も杓子も。
竜虎の母さんのブログ。 |
プロフィール
検索
gooおすすめリンク
発想の柔軟さ
2022年02月09日 / 塾
先日行われたある私立中学校の入試問題を解いていて、はたと手が止まった問題があった。

等しい辺に印を入れ、大きさの分かる角度は書きこんだ。
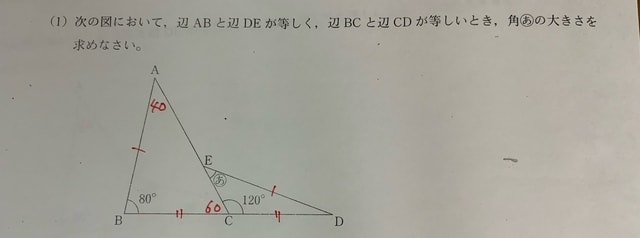
しかし、これ以上進まない。ちょっと考えて、
「ああ、そうか、等しい辺が重なるように一方の三角形を重ねてみればいいんだ」
と経験上思いついた。ならば、とこうやって移動してみた。

△A'B'C'という二等辺三角形ができて、ちょっといい感じかな、と思ったが、???「だから何!」という状態になってしまった。う~~ん、なかなかうまくいかない。案外難しい、困ったなあ・・。
などとブツブツ愚痴りながら、矯めつ眇めつ図を眺めていたら、はっと閃いた。
「そうか、三角形を上に重ねたからいけないんだ、下に重ねればいいんだ!」
早速試してみた。

素晴らしい!!なんと △A'B'Cが二等辺三角形となり、二等辺三角形の底角は等しいから、あ=∠A'=40°となる!!!解けた!
かなり嬉しかったけど、塾長ならこれくらい当たり前、問題見た瞬間にできなきゃダメだろう!と思う。
でも、自分としては多少の時間はかかっても、柔軟な発想ができたことが嬉しかった。
まだまだ俺も捨てたもんじゃないな、とちょっとばかり自信が湧いてきたのもまた嬉しかった。

等しい辺に印を入れ、大きさの分かる角度は書きこんだ。

しかし、これ以上進まない。ちょっと考えて、
「ああ、そうか、等しい辺が重なるように一方の三角形を重ねてみればいいんだ」
と経験上思いついた。ならば、とこうやって移動してみた。

△A'B'C'という二等辺三角形ができて、ちょっといい感じかな、と思ったが、???「だから何!」という状態になってしまった。う~~ん、なかなかうまくいかない。案外難しい、困ったなあ・・。
などとブツブツ愚痴りながら、矯めつ眇めつ図を眺めていたら、はっと閃いた。
「そうか、三角形を上に重ねたからいけないんだ、下に重ねればいいんだ!」
早速試してみた。

素晴らしい!!なんと △A'B'Cが二等辺三角形となり、二等辺三角形の底角は等しいから、あ=∠A'=40°となる!!!解けた!
かなり嬉しかったけど、塾長ならこれくらい当たり前、問題見た瞬間にできなきゃダメだろう!と思う。
でも、自分としては多少の時間はかかっても、柔軟な発想ができたことが嬉しかった。
まだまだ俺も捨てたもんじゃないな、とちょっとばかり自信が湧いてきたのもまた嬉しかった。
コメント ( 0 ) | Trackback ( 0 )





