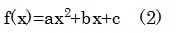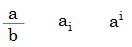英語と他の言語(11)から続く。
前回は、中学・高校レベルの数学の知識を前提に、日米両語で数式の読み方を紹介した。これで、簡単な数式が読めないという日本人の弱点を補強した。
次に問題になるのは、中身である。英語で数式の読み書きができるが、もし中身がお粗末であれば「TOEFLやTOEICはできるが、肝心の仕事ができない」ことの証し、これではビジネスの世界で胸を張って歩けない。
このことは、数学の問題だけでなく、コンピューター・プログラムや理路整然とした文章の作成といった分野にも当てはまる。
まず、数学的な思考過程を、下のヴェルトハイマーの問題【注1】で考える。
ヴェルトハイマーの問題

上の図は、正方形ABCDと、その上に横たわる帯状の平行四辺形EAFCの面積の和を求めるという問題である。
【注1:ヴェルトハイマー(M. Wertheimer, 1880-1943)はドイツのゲシタルト学派の心理学者で生産的思考(Productive Thinking)を提唱(1920年)。代表的な推論形式である三段論法では、第三段の結論は、第一段の大前提に含まれているものの反復にすぎず、何ら新しい認識を示さないと指摘した。三段論法に対して、生産的思考の結論では、前提とは異なった新しいものが生産されると説いた。上の図は、数学的推理の際にも生産的思考が営まれる例として使われた。】
ここで、ヴェルトハイマーの議論から外れるが、筆者はこの問題を使って次の実験を試みた。場所はアメリカのある大学、その図書館から出てくる人にこの問題を解いてもらった。一種のランダム・サンプリング、一人が終われば、次に出てくる人にお願いした。
男女年齢学歴国籍が異なる十数人の回答から、さまざまな考え方があることが分かった。また、皆さんが非常に協力的で嬉しかった。
回答の幾つかを要約すると次のようになる。
1)正方形ABCDの面積(a*a)+平行四辺形EAFCの面積((b-a)*a)=a*b 2)三角形EBCの面積+三角形ADFの面積=a*b/2+a*b/2=a*b 3)三角形EBCを下に平行移動して長方形ADFBに変形、その面積=a*b 4)小三角形EAD’【注2】と小三角形FCB’などと図を細かく分解し・・・。
【注2:D’は線分ADとECの交点、B’は線分BCとAFの交点。D’とB’は原題(上の図)には示されていない。】
問題に直面して、次々と考えを巡らして解決に向かう推論過程(思考)は興味深い。すべての人がa*bに到達したが、それぞれの回答から推論過程を分析した。推論過程が最も短いのは、「平行移動」→「a*b」、長いのは、「正方形ABCDの面積=a*a」→「小三角形のAD’の計算」→「b:a=(b-a):AD’」→「AD’の計算」→・・・など、さまざまだった。しかし、問題の処理スピードの点では、推論過程が短いほど効率的な方法といえる。ちなみに、この実験は教育訓練と効果測定という分野に発展させたが、ここでは詳細は省略する。
一つの問題に対して多様な解決方法があることは、コンピューター・プログラムの書き方にも言えることである。一つの問題を解くとき、短いプログラムで目的を果たす人、長いプログラムを書く人、考え方を整理せず、思い付くままに書き進み、そのうち迷路に入りいつまでもプログラムを完成できない人など、さまざまである。一般に、プログラムが短いほど単純明快で処理スピードが速く、ミスも少ない。
幸い、コンピューター・プログラムの場合は、パフォーマンスに問題があれば最適化手法で改善できる。したがって、事前にプログラミングの注意事項を初心者に教えれば、効率の悪いプログラムは避けられる。さらに、プログラムのロジックをフロー・チャート化すれば、理路整然とした分かり易いプログラムを作成できる。
話は変わるが、ビジネス文書の作成でも、コンピューター・プログラムと同じように、簡潔で分かり易い文章が求められる。当然、ビジネスの相手は世界の人々である。風俗習慣や言語の違いを超えた思考の共通ルール、それは人類共有の論理学、その論理で組み立てた考え方はどこの世界にも通用する。
世界共通の論理の具体例は、演繹法や帰納法、三段論法、ブール理論(真偽表)、確率論などである。これらの論理は、数学・電子工学・統計学などの理論と深い関係にあり、一見難しそうだが、中学・高校レベルの知識で十分に説明できる。さらに、頭の中にある考え方をフロー・チャートに変換すれば、意外に短時間で理路整然とした中身に整理できる。
ここで大切なことは、頭の中の考え方を論理的な文章に組み立てる。この作業はまず母語でマスターすべきである。母語で身に付けた文章力は、外国語にも利用できるので応用範囲が広くなる。
次回の(3)語学の学習に続く。