平成29年国家一般職（大卒）より。 ある二つの都市A、Bは、毎年度はじめに住民の統計調査を行っており、昨年度は、Aに住むB出身者が15万人であり、また、Bの総人口に占めるB出身者の割合は74％であることが分かった。その後、今年度の統計調査までに、 ①Aに住むB出身者のうち3万人がBへ転居し、また、 ②A、B以外の都市に住むB出身でない者のうち47万人がBへ転居した。 この結果、今年度のAの総人口は昨年度の95％となり、今年度のBの総人口に占めるB出身者の割合は70％となった。このとき、今年度の統計調査によると、Aの総人口とBの総人口の差は何万人か。 ただし、①及び②以外を原因とする、A、Bの人口変動はないものとする。😰 1. 769万人 2. 775万人 3. 781万人 4. 787万人 5. 793万人 まず、表を作ります。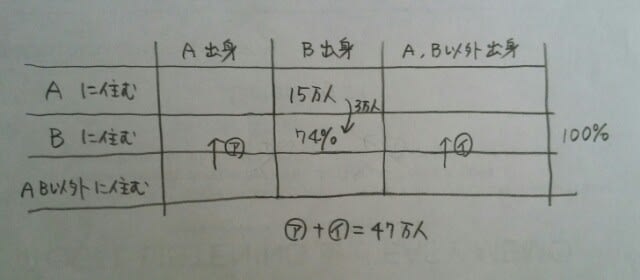
Bは大人気で、たったの1年で、3＋47＝50万人も人口が増加（一人も生まれず、一人も死ななければ）。昨年度のBの総人口をxとするのがよさそうですね。
今年度のBの総人口は、x＋50（万人）であり、そのうちの70％がB出身なので、0.7（x＋50）＝0.74x＋3。これを解くと、x＝800（万人）です。 また、Aは、減少した3万人が100－95＝5％に当たるので、昨年度は3×20＝60万人でした。 よって、今年度のAは60－3＝57万人。今年度のBは800＋50＝850万人。その差は850－57＝793万人で、正解は、肢5です。 それにしてもねえ。800万人もいて、一人も生まれず、一人も死なない都市なんて……。😵こんな統計調査など要らん！という人はここをポチッとお願いします。→
にほんブログ村
Bは大人気で、たったの1年で、3＋47＝50万人も人口が増加（一人も生まれず、一人も死ななければ）。昨年度のBの総人口をxとするのがよさそうですね。今年度のBの総人口は、x＋50（万人）であり、そのうちの70％がB出身なので、0.7（x＋50）＝0.74x＋3。これを解くと、x＝800（万人）です。 また、Aは、減少した3万人が100－95＝5％に当たるので、昨年度は3×20＝60万人でした。 よって、今年度のAは60－3＝57万人。今年度のBは800＋50＝850万人。その差は850－57＝793万人で、正解は、肢5です。 それにしてもねえ。800万人もいて、一人も生まれず、一人も死なない都市なんて……。😵こんな統計調査など要らん！という人はここをポチッとお願いします。→
にほんブログ村
図のように、A、B、Cに整数を一つずつ入力すると、DにはAとBの値の和を、EにはBとCの値の和を、FにはDとEの値の和を表示するプログラムがある。例えば、図Ⅱのように、Aに5、Bに7、Cに10を入力すると、Dには12、Eには17、Fには29が表示される。
A、B、Cに整数を一つずつ入力したところ、次のことが分かった。このとき、Fの値はいくらか。 ○Fの値はBの値の4倍である。 ○Eの値からAの値を引くと、8となる。 ○Eの値からDの値を引くと、2となる。 ①20②24③28④32⑤36 条件を式にすると、F＝4B…♤ E－A＝8…♢ E－D＝2…♡。 ♤より、Fは4の倍数です。選択肢は、当然4の倍数で揃えてありますね。 ♢より、E＝A＋8、♡より、E＝D＋2。ゆえに、A＋8＝D＋2。つまり、D＝A＋6です。 ところで、AにBを足したものがDなのだから、B＝6。これを♤に代入して、F＝24。正解は、肢②です。図で説明すると、
最後までやると、E＝A＋8だから、
ここをポチッとお願いします。→
皆さん、こんにちは。長年、公務員試験やら、教員採用試験やら、いろんな問題をみてきました。中には、これは何だ？？？というものもたくさんありました。中でも、ベスト（ワースト？）10に必ず入るであろう問題が、これです。 A君は7月初めから8月末の間に続けて夏休みを取った。夏休みの初めの10分の1に当たる日数を海辺で、次の10分の3に当たる日数を川辺で、続いて4日間を友人の家で過ごし、その翌日、山でチョウを捕まえたが、夏休みを数日残したある日、チョウは逃げてしまった。このとき、夏休みはチョウを捕まえた日から数えてチョウが逃げた日までの2倍の日数が経過していた。夏休みの日数として妥当なのはどれか。①10日②20日③30日④40日⑤50日 夏休みの日数の10分の1を海辺で過ごしたので、夏休みの日数は、当然10の倍数ですから、選択肢も全て10の倍数で統一されています。今、夏休みの日数を、10k日、チョウを捕まえてから、逃がしてしまうまでの日数をm（k、mは整数）として、図で表すと、
k＋3k＋4＝m。10k＞2m。よって、
k＝5で、夏休みは10×5＝50日。とでもするのでしょう。 ひょっとして、もう初めから気づいていた人も多かったと思いますが、もし、まだ気づいていない人は、問題文の、第1文と、最後の1文だけを読んで下さい。 7月初めから8月末までなら、選択肢上、50日しかありません。😵これは、平成8年度の国税専門官で出題されたと言われる問題でした。 ひょっとすると、機転をきかして、すぐに⑤を選びなさいという意図があったのかもしれませんが。 とにかく、初めて見たときは、驚きました。😓 このころは、試験問題は持って帰ることができない時代ですし、公務員試験自体、あまり注目されていなかったので、いわば、「ゆるゆる」なのですが、つい最近、国家一般職で、驚くべき１問が出ました。次回紹介します。ここをポチッとお願いします。→
すると、
肢①について…社会が60点ならば、
肢②について…リ＋シ＝150なのですから、リ＝35はあり得ません。（シ＝115点になってしまいます）肢③について…社会が70点ならば、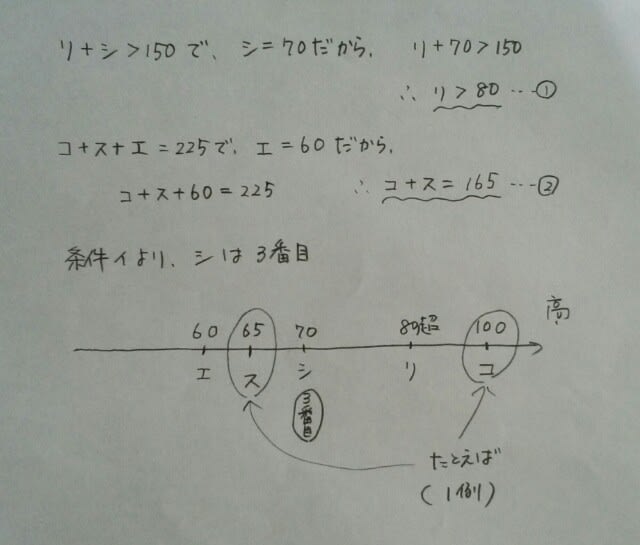
となって、これは可能性があります。 肢④について…コ＋ス＋エ＝225なのですから、ス＝40かつエ＝80ならば、コ＝105になってしまいます。 肢⑤について…リ＋シ＞150を満たさないので最悪。正解は、肢③です。
横の辺の長さが6mの長方形の部屋の床に正方形のタイルをしきつめる。横の辺に平行な直線で床を2つの長方形に分けて、一方には1辺が50cmのタイルをしき、もう一方には1辺が30cmのタイルをしくと、床全体にしきつめられる。このとき使うタイルは合計228枚である。 部屋のたての長さが横の長さより短いとき、部屋のたての辺の長さとして、最も妥当なのはどれか。①4.5m②4.6m③4.7m④4.8m⑤4.9m
1辺の長さが50cmのタイルをしきつめたとき、横には、600÷50＝12枚並びます。それがx段積み重なっているとすると、たての長さは、50（cm）がx段だから、50x（cm）。
1辺の長さが30cmのタイルをしきつめたとき、横には、600÷30＝20枚並びます。それがy段積み重なっているとすると、たての長さは、30cmがy段だから、30y（cm）。
タイルは合計228枚だから、
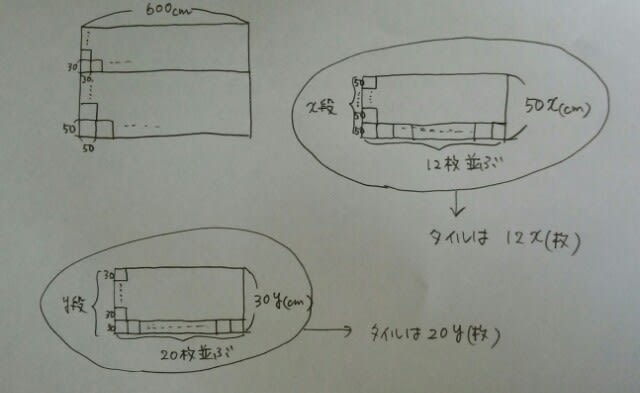どうやら、不定方程式のようです。
19－xが、5の倍数になるxを見つけていって、
xとyの組み合わせが3組見つかりました。アの場合は、もとの長方形のたての長さが50×4段＋30×9段＝470cm。たてが横より短いのでOK。イの場合は、50×9段＋30×6段＝630cmとなり、たてが横より長くなるのでダメ。ウもダメ。よって、たての長さは4.7m。正解は、肢③です。
