平成30年度警察官

下は割り算の筆算の一部を□で隠したものであり、□にはそれぞれ1桁の数字が入る。A、B、Cの和はいくらか。①20②21③22④23⑤24　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　九九の1の段、3の段、7の段、9の段の答えは、1の位がバラバラになっています。例えば、7の段の場合は、まず、無条件で決まるところは、□7×Cをしたときに、1の位が9なので、Cは7しかありません。また、よくみると、丸で囲ったところには、6しか入りません。すると今度は、□7×Bをしたときに、1の位が6なので、B＝8です。丸で囲った隣が3なので、割る数□7の□は6しかありません。よって、下の方はどんどん決まっていきます。すると、三角で囲ったところには、2しか入らないのですから、A＝6です。最後までやってみると、A＋B＋C＝6＋8＋7＝21。正解は、肢②です。ここをポチッとお願いします。→
にほんブログ村

歯車

次の図のように、軸が固定された3つの歯車A、B、Cがあり、歯の数は、それぞれ20、16、48である。Aの歯車が3分間で10回転する速さで回転し続けるとき、A、B、Cの歯車の矢印が次に同じように向き合うのは、何分何秒後か。（石川県教員採用試験、小学全科）　　　　　　　　　　　　　　　　　　　　　Aの歯車は、歯が20個ついているので、20個分進むごとに矢印は図の方向になります。　　　　　　　　　　　　　　　　　　　　　同様に、Bの歯車は16個分進むごとに、Cの歯車は48個分進むごとに矢印は図の方向になります。　　　　　　　　　　　　　　　　　　　　　よって、まずは、20と16と48の最小公倍数を求めて、240。　　　　　　　　　　　　　　　　　　　　それぞれの歯車が240個分進むと、再び図のようになります。　　　　　　　　　　　　　　　　　　　　　240÷20＝12より、Aが12回転すればよいのです。　　　　　　　　　　　　　　　　　　　　　Aは、3分で10回転ですから、18×12＝216秒＝3分36秒。　　　　　　　　　　　　　　　　　　　　正解は、3分36秒です。ここをポチッとお願いします。→
にほんブログ村

2019年度裁判所事務官no21

何の脈絡もなく手当たり次第に、適当な問題を、好き勝手に解説しています。　　　　　　　　　　　　　　　　　　　　2年もやっているのですが、こんなにやると、このブログで解説した問題と同じような問題が本番の試験でも出題されています。　　　　　　　　　　　　　　　　　　　「結構役に立ってるや～ん♬」と自画自賛。　　　　　　　　　　　　　　　　　　　　さて、先日の裁判所事務官でも、こんなやつがありましたよ！これは、2016年7月24日の「東京消防庁2類no18」の記事と、ほとんど同じです。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　異なる4つの整数から、2つずつ選んで和を求めたところ、27、38、49、50、61、72となった。この4つの整数のうち2番目に小さいものとして、確実に言えるものはどれか。①15②16③17④18⑤19　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4つの整数は、全て異なるので、小さい方から順に、a、b、c、dとします。　　　　　　　　　　　　　　　　　　　　例の記事に書いてあるように、2数の和は、上位2つと下位2つは決まり、その他は決まりません。　　　　　　　　　　　　　　　　　　　　よって、a＋b＝27、a＋c＝38、c＋d＝72、b＋d＝61は決定。　　　　　　　　　　　　　　　　　　　　a＋dとb＋cは、どちらかが49で、どちらかが50です。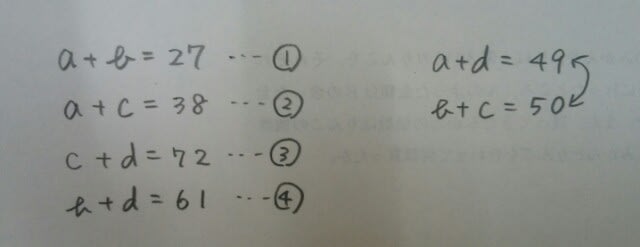ここから、好きなように計算していけば良いのですが、例えば、②－①をすると、c－b＝11。b＋cは、49か50ですが、仮に50だとすると、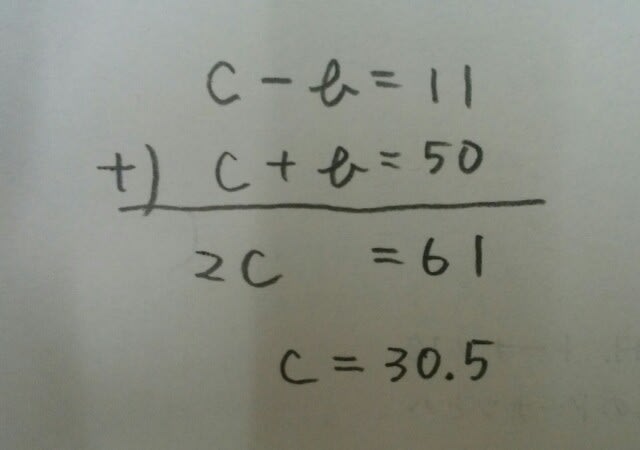ということになってしまい、cが整数ではなくなってしまいます。よって、b＋cは49です。（自動的にa＋d＝50）なので、2番目に小さいものはbなので、正解は、肢⑤です。ここをポチッとお願いします。→
にほんブログ村

どっちみち6枚だから…

3日前は、国税専門官の本試験が行われ、昨日京都校に行くと、質問攻めにあいました。　　　　　　　　　　　　　　　　　　　　それにしても、テレビのチャンネルのやつは難問でしたねえ。あんなのは、捨て問題だと思いますよ。　　　　　　　　　　　　　　　　　　　　さて、その中から1問。no22です。　　　　　　　　　　　　　　　　　　　　図のように、縦6行、横10列で60枚のラベルが並んだシートがたくさん用意されている。これらのシートのラベルに、次のルールで数字を印字する作業を行うこととする。　　　　　　　　　　　　　　　　　　　　　［ルール］　　　　　　　　　　　　　　　　　　　　①各シートにおいて、一番右側の列にあるラベルに上から順に数字を印字し、印字し終えたら、一つ左側の列にあるラベルに上から順に数字を印字する。（図の矢印）　　　　　　　　　　　　　　　　　　　　②　①を繰り返し、一番左側の列にある全てのラベルに数字を印字し終えたら、次のシートに取り替えて、同様に印字する。　　　　　　　　　　　　　　　　　　　③数字は、1、2、…、44の44個の整数とする。また、値の小さい方から順に印字し、44の次は再び1に戻る。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ところが、5枚目のシートにある全てのラベルに印字し終えた段階で数字を確認したところ、それまでの作業は③ではなく次の③’に基づいていることが分かった。　　　　　　　　　　　　　　　　　　　　　③’数字は、1、2、…、45の45個の整数とする。また、値の小さい方から順に印字し、45の次は再び1に戻る。　　　　　　　　　　　　　　　　　　　　　そこで、6枚目以降のシートは、①、②、③に基づいて、改めて、シートの一番右上のラベル（一番右側の列にあるラベルで一番上にあるもの）に印字する数字を1として、印字を行い、シートの一番左下のラベル（一番左側の列にあるラベルで一番下にあるもの）に初めて44が印字された時点で、作業を終えた。作業を終えた時点で、44が印字されたラベルの枚数は、1～5枚目のシートにある44が印字されたラベルも含めて全部で何枚か。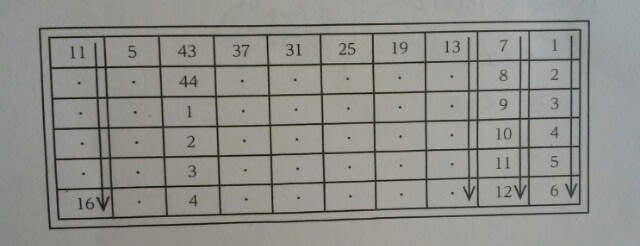①17枚②21枚③25枚④29枚⑤33枚　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　かなり長文ですが、要するに、「5枚目まで作業をしたら、ちょびっとミスってたことに気づいたので、6枚目以降はミスらずにやりましたよ」ということですね。（このちょびっとがポイント）　　　　　　　　　　　　　　　　　　　　　　　1枚のシートには、60個印字するので、5枚作業をすると、60×5＝300個印字します。　　　　　　　　　　　　　　　　　　　　　　　このとき、③のルールを守っていれば、300÷44＝6余り36なので、「44」は、6回印字され、5枚目の左下には36という数字が印字されていたはずです。　　　　　　　　　　　　　　　　　　　　　　　繰り返しますが、ここがポイントです。　　　　　　　　　　　　　　　　　　　　　　「では、いつルール③からルール③’になったの？」とか、「5枚目の左下の数字は何？」ということが気になりますが、正解は、「いつでも、そして何番でもよろしい」です。ルール③とルール③’では、数字は1しか違わないからです。（ただし、最後が1とか2付近でで終わるはずだった場合は、よく調べてみないといけませんが）　　　　　　　　　　　　　　　　　　　　　　　ここまでまとめますと、　　　　　　　　　　　　　　　　　　　　　　　★5枚目までに「44」は、6回印字されている。　　　　　　　　　　　　　　　　　　　　　　　★いつ③から③’になったとしても、「44」が6回印字されていることには変わりがない　　　　　　　　　　　　　　　　　　　　　　　　★もっと言えば、選択肢を見れば、1枚くらいずれたとしても、十分正解の選択肢は見つかる。ということです。　　　　　　　　　　　　　　　　　　　　　　　さて、6枚目以降です。　　　　　　　　　　　　　　　　　　　　　　　1枚のシートには60箇所印字する場所があって、、印字は44までで1セットだから、60と44の最小公倍数を計算して、660。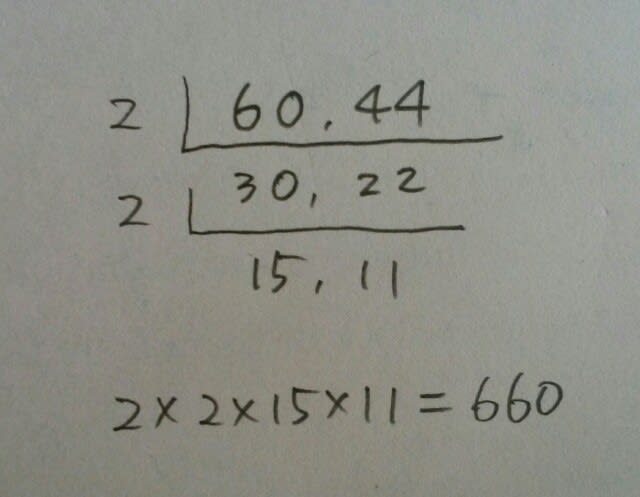660÷44＝15。6枚目以降には、「44」は、15枚あります。よって、1から5枚目のシートには6枚、6枚目以降には15枚、合わせて21枚。正解は、肢②です。　　　　　　　　　　　　　　　　　　　　本問は、いつルールが切り替わっても、それは正解とは関係ない！気にするなよ！ということでしたが、これに似た問題、国家公務員ではたまに見かけます。地方公務員ではほとんど無かったと思います。それでも気になる気になる！という人は、以下を参照して下さい。やはり、5枚目の左下の数字が1ずつ変化するだけで、どっちみち「44」が6枚であることが分かりますね。そして、たとえこれが実は5枚になったり7枚になったりするとしても、選択肢を見ると、1枚くらい事実と違っていても、正解の選択肢は選べるという状況になっていますね。ここをポチッとお願いします。→
にほんブログ村

自然数を3等分すると……

世の中にある全ての自然数（1以上の整数）を、2等分するには、奇数と偶数に分ければよく、日常の生活でもよく使います。　　　　　　　　　　　　　　　　　　　では、3等分（3種類に分けるでも可）するには、どうすればいいのでしょうか？　　　　　　　　　　　　　　　　　　　2018年度岩手県教員採用試験小学全科より。　　　　　　　　　　　　　　　　　　　　nを自然数とするとき、nの2乗を3で割ったときの余りについて、正しいものを次のア～エから一つ選び、その記号を書きなさい。　　　　　　　　　　　　　　　　　　　　ア　1または2　　イ　0または1　　ウ　0または2　　エ　2　　　　　　　　　　　　　　　　　　　　　　全ての自然数を3つに分類するには、①3で割り切れるもの②3で割ると1余るもの③3で割ると2余るものに分けると便利です。　　　　　　　　　　　　　　　　　　　　奇数と偶数も、難しい言い方をすれば、①2で割り切れるものと、②2で割ると1余るものという分け方ですね。　　　　　　　　　　　　　　　　　　　　さて、ある自然数nが、グループ①の、3で割り切れるものだったら、nの2乗を3で割ったときの余りはいくつでしょうか？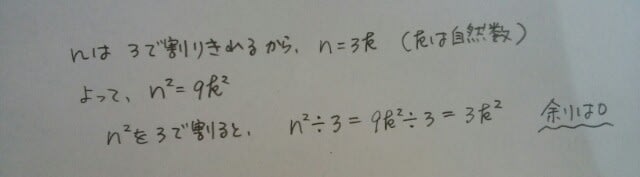ある自然数nが、グループ②の、3で割ると1余るものだったら、グループ③だったら、これで、全ての自然数について考えたことになります。あまりは、0か1にしかなりません。正解は、肢イです。ここをポチッとお願いします。→
にほんブログ村