図1のような長方形の紙を、図2のように短い方の辺が長い方の辺に重なるように折り曲げ、折り目をつけて元に戻す。これを四隅について行うと図3の点線のような折り目ができた。このとき、図4の網掛けで示された四角形の面積が50㎠、三角形の面積が64㎤であった。図1の長方形の長い方の辺の長さはいくらか、下のア～オから一つ選びなさい。
たての長さを、xとすると、x＝16です。その理由は、
また、網掛けの四角形は正方形で、面積は、（対角線）×（対角線）÷2です。正方形の対角線は同じ長さなので、これをyとして、
よって、
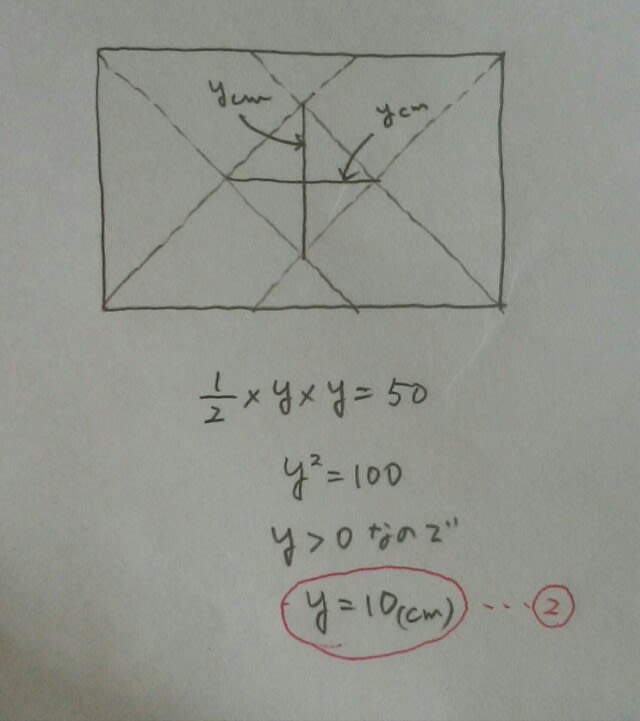
正解は、肢エです。
次の図は、底面の半径が2cmで高さがxcmの円すいと半径が2cmの半球を組み合わせた立体である。この立体の体積が12π㎤であるとき、xの値として最も適切なものを、後の①～⑤のうちから選びなさい。ただし、円周率はπとする。
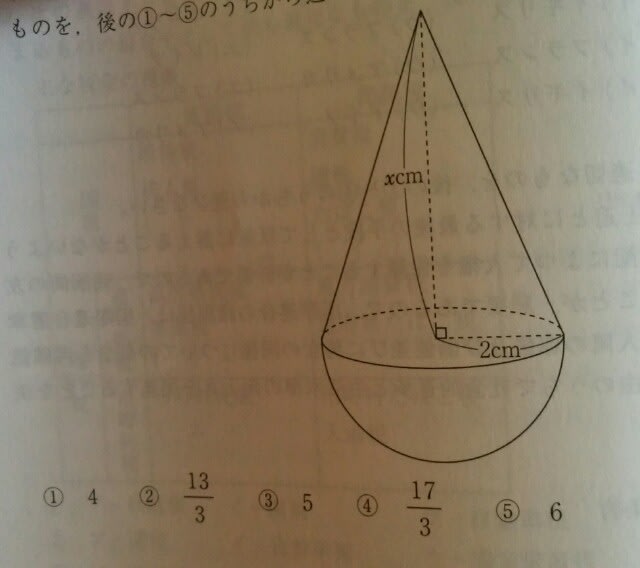球と、円すいに関する公式は、
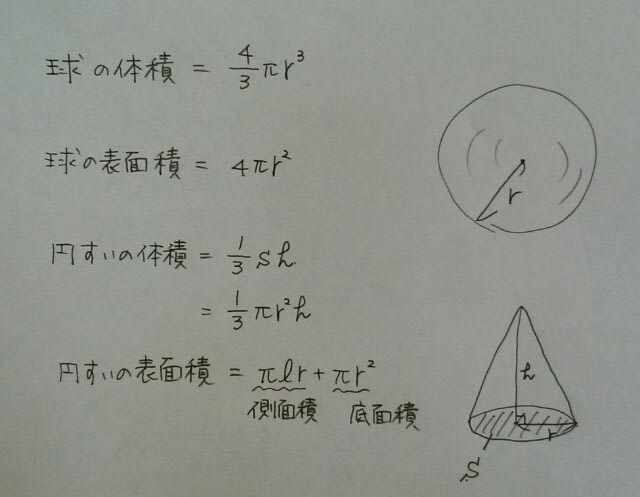本問は、立体の体積が12πなので、方程式を作ります。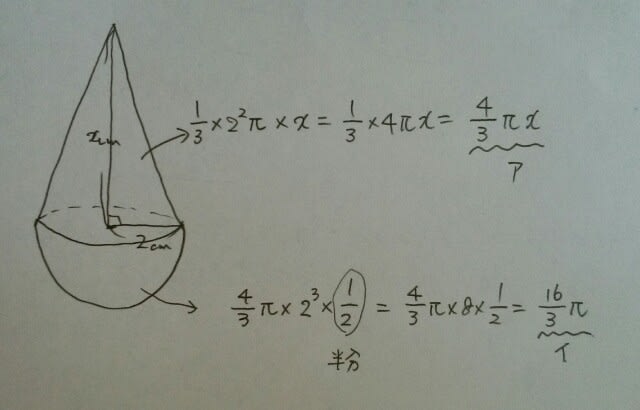
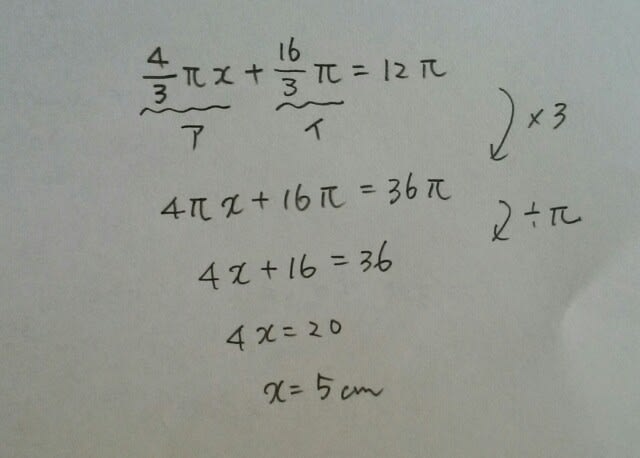正解は、肢③です。
次の図の斜線部分の面積として、最も妥当なのはどれか。
気が付けば簡単ですが、変な方向に行くと、分からなくなってしまいます。
それから、
なので、4＋13＝17㎠。正解は、肢4です。
下の図のように、線分ABと線分CDは平行で、線分ADと線分BCの交点をEとします。点Fは線分CD上の点で、線分EFと線分BDは平行です。AB＝3cm、BD＝4cm、CD＝5cmであるとき、線分EFの長さとして正しいものを、次の1～4の中から1つ選びなさい。
相似な三角形を探します。
さらに、相似な三角形を探します。
正解は、肢3です。
三角形を分割したときの面積比の定理。
本問の場合は、
ということになり、正解は、肢②です。
