国家一般職の判断推理 1

2021年出題。　　　　　　　　　　　　　　　　　　　　　　　　あるクラスで水泳、バレーボール、テニス、野球、弓道、サッカーの6種類のスポーツについてアンケートをとった。　　　　　　　　　　　　　　次のことが分かっているとき、確実にいえることとして最も妥当なのはどれか。　　　　　　　　　　　　◯バレーボールが好きではない人は、野球が好きである。　　　　　　　　　　　　　　　　　　　　　◯テニスが好きな人は、水泳が好きではない。　　　　　　　　　　　　　　　　　　　　　　　　　◯サッカー又はバレーボールが好きな人は、テニスが好きである。　　　　　　　　　　　　　　　◯サッカーが好きではない人は、弓道が好きである。　　　　　　　　　　　　　　　　　　　　　①水泳が好きな人は、弓道が好きである。　　　　　　　　　　　　　　　　　　　　　　　　　②バレーボールが好きな人は、弓道が好きである。　　　　　　　　　　　　　　　　　　　③テニスが好きな人は、野球が好きである。　　　　　　　　　　　　　　　　　　　　　　④野球が好きな人は、水泳が好きである。　　　　　　　　　　　　　　　　　　　　　　　　⑤サッカーが好きな人は、水泳が好きである。　　　　　　　　　　　　　　　　　　　　　　　　　　条件を書き出すと、
対偶もつくっておきます。
選択肢①を調べると、
このように、いきなりこれが正解でした。　　　　　　　　　　　　　　　　　　　　　　　　選択肢②は、バレーボールが好きな人は、水泳が好きではないということはいえますが、弓道が好きかどうかは不明。
選択肢③は、テニスが好きな人は、水泳が好きではないということはいえますが、野球が好きかどうかは不明。　　　　　　　　　　　　　　選択肢④は、野球が好きな人がどうなのか、全く不明。　　　　　　　　　　　　　　　　　　　選択肢⑤は、サッカーが好きな人は、必ず水泳は好きではないので、間違いです。
正解は、肢①です。

国家一般職の数的推理 5

2021年の第５問も整数からの出題でした。今年は、５題のうち３題が整数というかなり偏った出題でした。　　　　　　　　　　　　　　北米には13年ゼミと17年ゼミといわれる、周期的に一斉に成虫が発生するセミがいる。これらのセミは、卵が生まれてから成虫になるまで13年又は17年を要し、それぞれ13年目、17年目に成虫になる。　　　　　　　　　　　　　　　　13年ゼミは3系統あり、それぞれの系統は13年目に成虫になるが、成虫になる年は全て異なり、13年のうち3年はいずれかの系統の成虫が発生している。　　　　　　　　　　　例えば、2021〜2033年の13年のうち、成虫が発生するのは2024年、2027年、2028年の3年だけである。　　　　　　　　　　　　　　　　同様に、17年ゼミは12系統あり、17年のうち12年はいずれかの系統の成虫が発生している。　　　　　　　　　　　　　　　　　　　　　　　　2021年以降、最初に13年ゼミの3系統、17年ゼミの12系統の成虫が発生する予定の年は次のとおりであり、その後もそれぞれの系統は13年又は17年ごとに成虫が発生することが見込まれている。なお、セミは成虫となった年までしか生きることができない。
ここで、2021〜2250年の230年間に、13年ゼミの成虫のみが発生する年は何年あるかを次のようにして考えたとき、A、B、Cに当てはまるものの組合せとして最も妥当なのはどれか。　　　　　　　　　　　　　　　　　　　　「ある系統の13年ゼミの成虫が発生するのは13年に1回であり、2021〜2250年の間に13年ゼミの3系統のいずれかが発生している年はA回である。一方、ある系統の13年ゼミとある系統の17年ゼミの両方が発生するのは221（＝13✕17）年に1回であり、2021〜2250年の間に13年ゼミの3系統合計でみると、13年ゼミと17年ゼミの両方が発生する年は、B回である。よって、13年ゼミのみが発生する年はC回である。」
少し細かいことですが、一つ確認しておきます。　　　　　　　　　　　　　　　　　　　一般に、A年からB年までは、B−A＋1年あります。例えば、「2018年から2022年まで病気のために休職していました」という場合、普通、2018年の1月1日から2022年の12月31日までと考えるので、2022−2018＋1＝5年間休職していたということですね。だから、2021年〜2250年は230年間です。　　　　　　　　　　さて、この230年間に13年は何回あるかというと、230÷13＝17あまり9なので、17回あって、さらに9年あります。また、13年ゼミは3系統あって、3系統ともバラバラの年に発生するのだから、Aは、こうなります。
13年ゼミの3系統を、それぞれ、13−1、13−2、13−3、また、17年ゼミの12系統を、それぞれ、17−1、17−2、………17−12としましょう。　　　　　　　13−1と17−1は、221年に一度だけ同時に発生します。また、13−2と17−1も、221年に一度だけ同時に発生します。また、13年ゼミと17年ゼミの組合せは3×12＝36組。　　　　　　　　　　　　　　　そして13年ゼミの3系統はバラバラの年に発生し、17年ゼミの12系統もバラバラの年に発生します。よって、221年間にある種類の13年ゼミとある種類の17年ゼミが同時に発生する年は36年（回）。BとCはこうなります。
正解は、肢4です。　　　　　　　　　　　♬人生はいつでも山あり谷ありで休みもなし上をみて下と比べ自分の位置考えちゃう♫

国家一般職の数的推理 4

2021年の第4問は、第2問と同じく、整数問題でした。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　AとBの2人がおり、Aは10〜99の二桁の整数のうちから一つの数を頭に思い浮かべ、Bはその数を当てようとして「はい」か「いいえ」で答えられる質問を、次のとおり行った。　　　　　①「その数は、ある整数を二乗した数から3を引いた数と等しいか？」と聞いたところ、Aは正しく「はい」と答えた。　　　　　　　　　　次に、Bは候補を絞る質問として、次の二つの質問をしたが、Aは二つとも嘘を答えた。　　　　　　　　　　　　 ②「その数は、40より大きいか？」 　　　　　　　　　　　　　　　　　　　③「その数は、奇数か？」　　　　　　　　　　　　　　Bは、これら三つの質問に対するAの答えが全て正しいものとして推論を行ったが、数の候補は複数あった。そこで、これを一つに絞る質問として、次の質問を行った。　　　　　　　　　　　　　　　　　④「その数は、十の位と一の位の数を足すと7より大きいか？」このとき、Aが頭に思い浮かべた数はどれか。

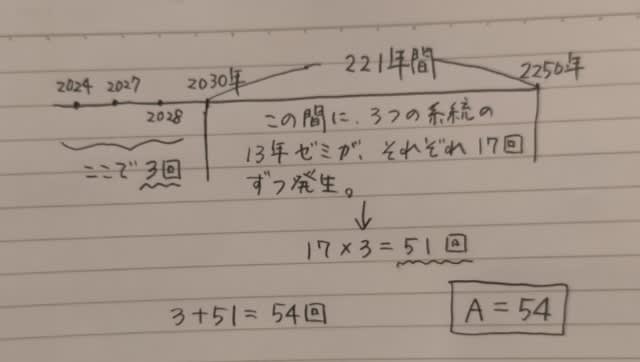
①の質問には、Aは正しく「はい」と答えたので、Aが頭に思い浮かべた数は、二桁で、かつある整数を二乗した数から3を引いた数です。　　　　　　　　　　　　　つまり、13か22か33か46か61か78か97ですね。　　　　　　　　　　　　　　　　　質問②と③に対してAがどう答えたのかが問題です。整理しましょう。次に、Aがどう答えたかと、その時Bはどう推論するかを整理します。
このとき、数の候補は複数あったのだから、㋓はダメで、㋐か㋑か㋒ですね。　　　　　　そこでBは、「これを一つに絞る質問として」④の質問をしたのです。　　　　　　　　　　㋑のときに④のような質問をしたら、Bはアホです。　　　　　　　　　　　　　　　　　そんな質問をしても、Aが「はい」と答えても46か78か分からず、結局一つに絞れないし、「いいえ」と答えたら、「お前ええかげんにしろよ、嘘つくな」ということになる。　　　　　　　　　　　　　　㋒のときも同様ですね。　　　　　　　　　　　　だから、㋐だったわけです。　　　　　　　　　よって、Aが頭に思い浮かべた数は61か97で、このうち選択肢にあるのは５なので、正解は５などとやってしまうと、まんまとA（あるいは出題者）に嵌められたことになります。　　　　　　　　　　　　　　②と③にAは嘘をついている。　　　　　　　　　Aは、㋐のように答えた（②に「はい」③に「はい」）のだから、Aが嘘をつかなかったら、どちらの質問に対しても「いいえ」と答えます。問題文に、「Aは二つとも嘘を答えた」と書いてあります。　　　　　　　　　　　　　　　　　　②にも③にも「いいえ」だったら、図の㋓。つまり、Aが頭に思い浮かべた数は22だったのです。　　　　　　　　　　　　　　　　　　正解は肢2です。　　　　　　　　　　　　　　　　見ざる聞かざる言わざるでござる　人生受け身は今日で終わらせるよgoodbye!

国家一般職の数的推理 3

2021年の第3問は、図形からの出題でした。図のように、一辺の長さが1の正方形Aに内接し、30°傾いた正方形を正方形Bとする。また、正方形Bに内接し、45°傾いた長方形の長辺をa、短辺をbとする。aとbの長さの比が2:1であるとき、aの長さはいくらか。





図の中には、2種類の三角定規が4つずつあり、大きさも考慮すると、3種類あることになります。つまり、
三角定規の辺の比について確認すると、
ですね。それでは、解説を始めます。赤い三角形と青い三角形は、どちらも直角二等辺三角形（1:1:√2の三角定規）で、相似です。aとbの長さの比が2:1ということは、赤い三角形のそれぞれの長さを2 倍したものが青い三角形だということ。いま、AC＝BC＝kとすると、BE＝DE＝2kだから、EC＝3k。

さらに、△ECFと△HEGは合同

だから、GE＋EF＝CF＋EF。△ECFは、1:2:√3の三角定規です。だから、さて、求めるものはaの長さですので、もう一度赤い三角形に戻る必要があります。
bは、図の①なので、b＝√2k。aは、図の②なので、a＝2√2k。よって、
正解は、肢4でした。

レッツパーティーだ!

国家一般職（大卒）の数的推理 2

2021年実施の第2問は、整数分野からの出題でした。　　　　　　　　　　　　　　　　　　　　0又は1桁の正の整数a、bを用いて次のように表される4桁の数がある。この数が7と11のいずれでも割り切れるとき、aとbの和はいくらか。選択肢省略。　　　　　　　　　　　　　　　　7と11のいずれでも割り切れるのだから、この数は7と11の公倍数、つまり77の倍数ですね。ポイントは、1の位の数です。　　　　　　　　　　　　　　　　　小学校で、九九を習いました。なかなか覚えられず、泣きそうになりましたね。本当に泣き出す子もいたりして、今なら先生は優しく励ましてくれるのでしょうが、我々昭和30年、40年代生まれの子供たちは、何で覚えられないの?もっとしっかり勉強しなさい!と怒られるばかり。　特に7の段が覚えにくく、7×6＝54?7×8＝42？何かぐちやぐちゃぐちゃや〜、。ということになってました。この僕は。

それはさておき、九九の1、3、7、9の段には、ある特徴があるのですが、分かりますか?1の位の数がバラバラになっているのです。例えば、7の段では、
なので、掛け算や割り算の計算パズルでは、この1、3、7、9がよくキーナンバーとなります。　　　さて、ごちゃごちゃ言わずに解説していきましょう。　　　　　　　　　　　　　　　　　2□□4は77を何倍かした数です。大雑把に、30倍か40倍くらいした数です。（77×30＝2310、77×40＝3080）もしかしたら、20何倍かもしれません。　　　　　　　　　　　　　　77の1のくらいの「7」に何を掛けたら2□□4の1の位の「4」になるか?「2」しかありませんね。だから、多分32倍でしょう。　　　　　　実際にやってみると、77×22＝1694で、2000にもいかない。77×32＝2464でピッタリ。77×42＝3234で3000台になる。　　　　　よって、a＝4、b＝6。aとbの和は10です。
震える身体これが武者震い限界を越えて存在価値みせろ　OK?