下図で、3つの円の半径は等しく、それぞれほかの2つの円の中心を通っている。3つの円の半径が3√6cmのとき、色をつけた部分の面積の合計はいくらか。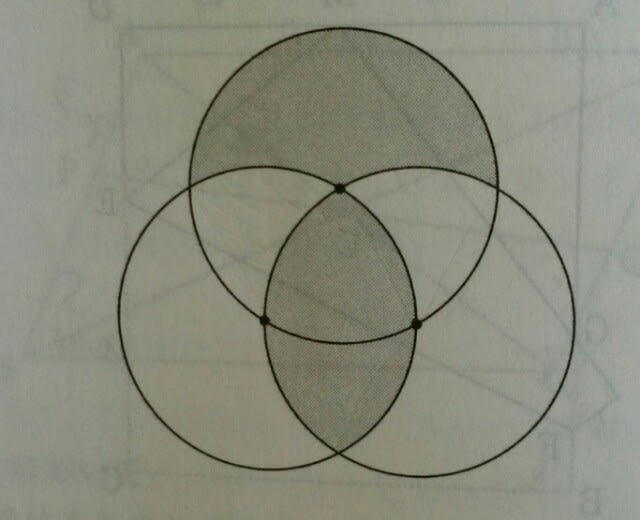 (三重県教員採用試験) 出した物は出しっぱなし、授業で使ったプリントも、どこかへいってしまって、次の授業前、「あのプリントどこや?」と探しまくって、結局出てこない。ホントに情けなくなります。(私のこと) なので、こういう問題は苦手です。斜線部分を、矢印で示した場所にお片づけ~。
(三重県教員採用試験) 出した物は出しっぱなし、授業で使ったプリントも、どこかへいってしまって、次の授業前、「あのプリントどこや?」と探しまくって、結局出てこない。ホントに情けなくなります。(私のこと) なので、こういう問題は苦手です。斜線部分を、矢印で示した場所にお片づけ~。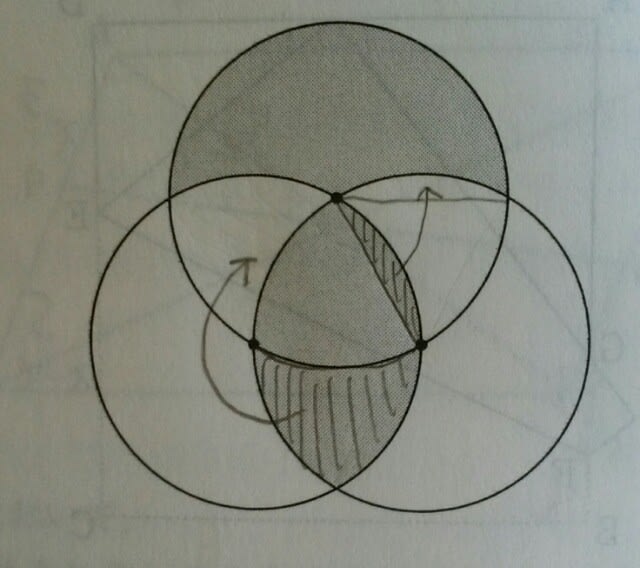 すると、
すると、 すっきりり~ん。
すっきりり~ん。 r1とr2は、上の円の半径、r3は、右下の円の半径で、全ての円の半径は等しいのだから、r1=r2=r3。パックマンのお口は60º開いています。よって、求める面積は、
r1とr2は、上の円の半径、r3は、右下の円の半径で、全ての円の半径は等しいのだから、r1=r2=r3。パックマンのお口は60º開いています。よって、求める面積は、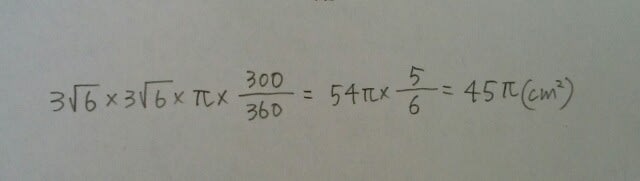 正解は、45π㎠です。ここをポチッとお願いします。→
正解は、45π㎠です。ここをポチッとお願いします。→
にほんブログ村

 (三重県教員採用試験) 出した物は出しっぱなし、授業で使ったプリントも、どこかへいってしまって、次の授業前、「あのプリントどこや?」と探しまくって、結局出てこない。ホントに情けなくなります。(私のこと) なので、こういう問題は苦手です。斜線部分を、矢印で示した場所にお片づけ~。
(三重県教員採用試験) 出した物は出しっぱなし、授業で使ったプリントも、どこかへいってしまって、次の授業前、「あのプリントどこや?」と探しまくって、結局出てこない。ホントに情けなくなります。(私のこと) なので、こういう問題は苦手です。斜線部分を、矢印で示した場所にお片づけ~。 すると、
すると、 すっきりり~ん。
すっきりり~ん。 r1とr2は、上の円の半径、r3は、右下の円の半径で、全ての円の半径は等しいのだから、r1=r2=r3。パックマンのお口は60º開いています。よって、求める面積は、
r1とr2は、上の円の半径、r3は、右下の円の半径で、全ての円の半径は等しいのだから、r1=r2=r3。パックマンのお口は60º開いています。よって、求める面積は、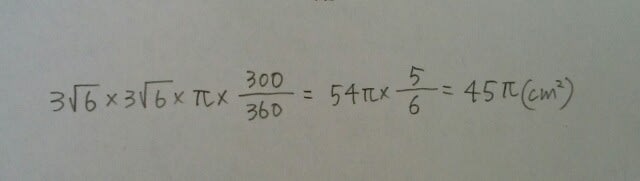 正解は、45π㎠です。ここをポチッとお願いします。→
正解は、45π㎠です。ここをポチッとお願いします。→にほんブログ村











