ある中学1年生Aさんの1学期の期末考査(国語、社会、数学、理科、英語 各教科100点満点)の得点について、次のア~エのことが分かっている。 ア、国語、数学、英語の3教科の平均点は、75.0点である。 イ、社会の得点は、5教科のなかで3番目に高い。 ウ、5教科の平均点は、75.0点より高い。 エ、5教科の得点は、すべて異なる得点である。 このとき、この考査におけるAさんの得点として、可能性があるものはどれか。1~5から一つ選べ。 ①国語の得点が70点かつ社会の得点が60点 ②国語の得点が90点かつ理科の得点が35点 ③社会の得点が70点かつ英語の得点が60点 ④数学の得点が40点かつ英語の得点が80点 ⑤理科の得点が50点かつ社会の得点が90点 国語=コ、数学=ス、英語=エ、理科=リ、社会=シとします。国語と数学と英語の平均点が75なので、コ+ス+エ=75×3=225。5教科の平均点が75より高いので、コ+ス+エ+シ+リ>75×5=375ですね。 すると、
すると、 肢①について…社会が60点ならば、
肢①について…社会が60点ならば、 肢②について…リ+シ=150なのですから、リ=35はあり得ません。(シ=115点になってしまいます)肢③について…社会が70点ならば、
肢②について…リ+シ=150なのですから、リ=35はあり得ません。(シ=115点になってしまいます)肢③について…社会が70点ならば、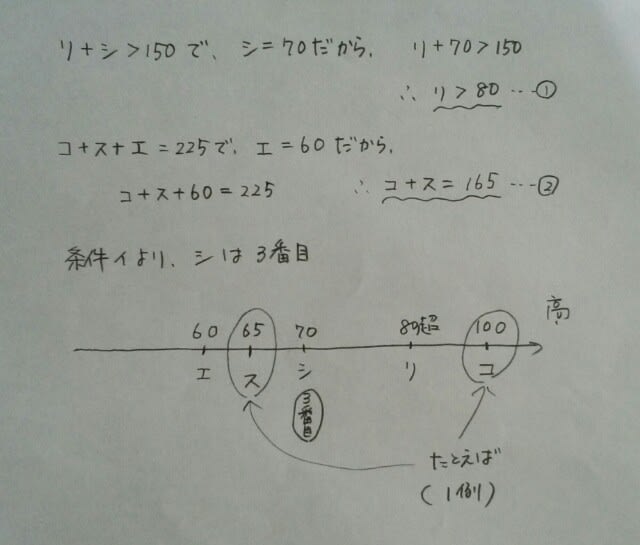 となって、これは可能性があります。 肢④について…コ+ス+エ=225なのですから、ス=40かつエ=80ならば、コ=105になってしまいます。 肢⑤について…リ+シ>150を満たさないので最悪。正解は、肢③です。
となって、これは可能性があります。 肢④について…コ+ス+エ=225なのですから、ス=40かつエ=80ならば、コ=105になってしまいます。 肢⑤について…リ+シ>150を満たさないので最悪。正解は、肢③です。

 すると、
すると、 肢①について…社会が60点ならば、
肢①について…社会が60点ならば、 肢②について…リ+シ=150なのですから、リ=35はあり得ません。(シ=115点になってしまいます)肢③について…社会が70点ならば、
肢②について…リ+シ=150なのですから、リ=35はあり得ません。(シ=115点になってしまいます)肢③について…社会が70点ならば、 となって、これは可能性があります。 肢④について…コ+ス+エ=225なのですから、ス=40かつエ=80ならば、コ=105になってしまいます。 肢⑤について…リ+シ>150を満たさないので最悪。正解は、肢③です。
となって、これは可能性があります。 肢④について…コ+ス+エ=225なのですから、ス=40かつエ=80ならば、コ=105になってしまいます。 肢⑤について…リ+シ>150を満たさないので最悪。正解は、肢③です。











 条件エがポイントです。観光目的ではない=仕事目的。仕事目的ではない=観光目的。ということになりますね。よって、
条件エがポイントです。観光目的ではない=仕事目的。仕事目的ではない=観光目的。ということになりますね。よって、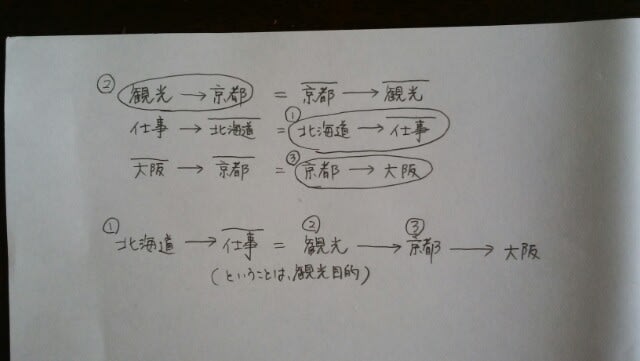 正解は、肢④です。因みに、肢①北海道に行く外国人は、必ず京都に行きます。肢②大阪に行かない外国人は、絶対に北海道には行きません。肢③観光目的の外国人は、必ず大阪に行きます。肢⑤仕事が目的の外国人は、大阪に行くかどうかは分かりません。
正解は、肢④です。因みに、肢①北海道に行く外国人は、必ず京都に行きます。肢②大阪に行かない外国人は、絶対に北海道には行きません。肢③観光目的の外国人は、必ず大阪に行きます。肢⑤仕事が目的の外国人は、大阪に行くかどうかは分かりません。
 1組で現在はAコースだが来学期はBコースを希望する児童が4人であり、2組で現在はBコースだが来学期はAコースを希望する児童が3人であることが分かっている。このとき、この6年生の2学級において、来学期のコース希望が、現在のコースと異なるコースを希望する児童の総数として正しいものはどれか。1~5から一つ選べ。①8人②12人③15人④19人⑤25人 まずは、1組、2組の様子を表に整理します。
1組で現在はAコースだが来学期はBコースを希望する児童が4人であり、2組で現在はBコースだが来学期はAコースを希望する児童が3人であることが分かっている。このとき、この6年生の2学級において、来学期のコース希望が、現在のコースと異なるコースを希望する児童の総数として正しいものはどれか。1~5から一つ選べ。①8人②12人③15人④19人⑤25人 まずは、1組、2組の様子を表に整理します。 ここに、問題文の、数表より下に書いてある人数を記入すると、
ここに、問題文の、数表より下に書いてある人数を記入すると、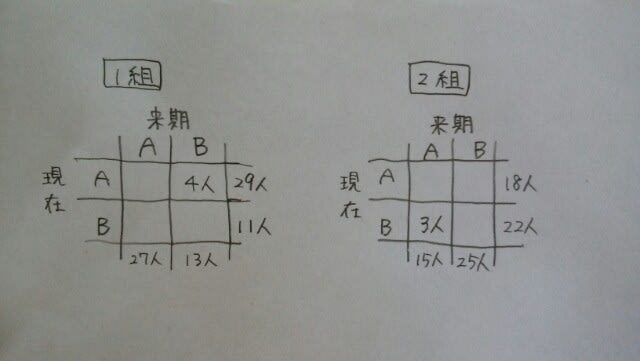 例えば、1組で、現在はAコースで、来学期もAコースを希望する児童は、29-4=25人。という風に、引き算していくと、全ての空欄が埋まります。
例えば、1組で、現在はAコースで、来学期もAコースを希望する児童は、29-4=25人。という風に、引き算していくと、全ての空欄が埋まります。 来学期のコース希望が、現在のコースと異なるものは、
来学期のコース希望が、現在のコースと異なるものは、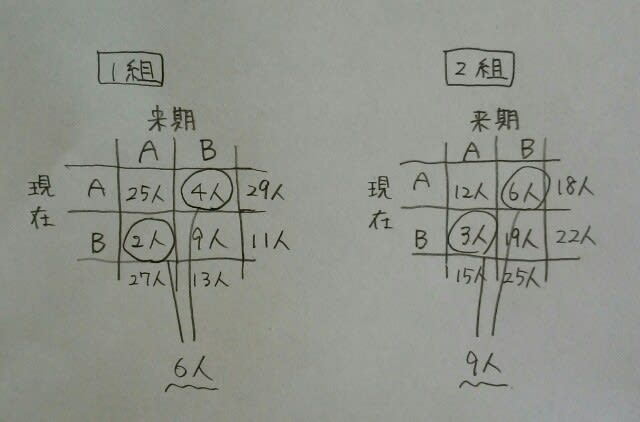 よって、6+9=15人です。正解は、肢③です。
よって、6+9=15人です。正解は、肢③です。
 1日目は、D対F、B対Aが行われたので、自動的にもう1試合はC対Eですね。その試合にCは勝ちました。
1日目は、D対F、B対Aが行われたので、自動的にもう1試合はC対Eですね。その試合にCは勝ちました。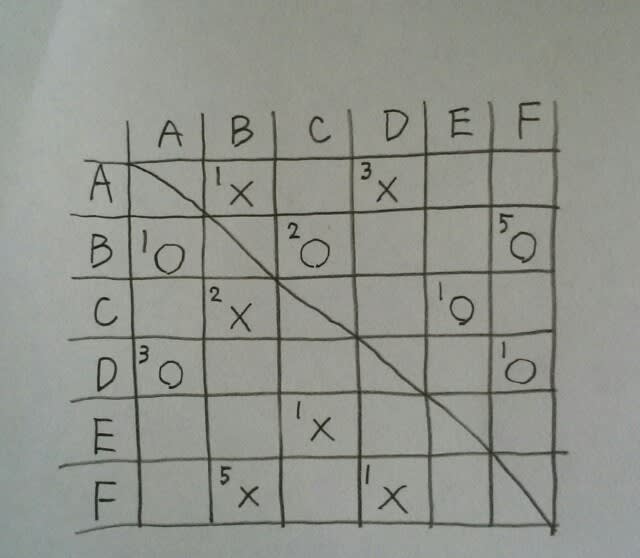 あとは、練習問題①でやったように、してみて下さい。例えば、B対Dの試合は、1日目でも、2日目でも、5日目でも、3日目でもないので、4日目です。(縦、横で、同じ数字がダブらないようにする。)その結果、こうなります。
あとは、練習問題①でやったように、してみて下さい。例えば、B対Dの試合は、1日目でも、2日目でも、5日目でも、3日目でもないので、4日目です。(縦、横で、同じ数字がダブらないようにする。)その結果、こうなります。 ここに、条件に書いてある試合結果を書き込むと…
ここに、条件に書いてある試合結果を書き込むと… 今度は、練習問題②でやったことを思い出して下さい。引き分けなしで、全員違う成績なので、全勝したのはB、全敗したのはF…
今度は、練習問題②でやったことを思い出して下さい。引き分けなしで、全員違う成績なので、全勝したのはB、全敗したのはF…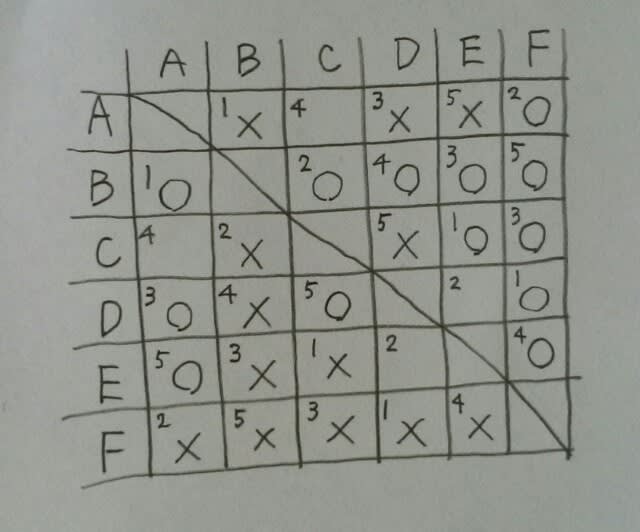 ここで、DがEに負けてしまうと、2チームとも3勝2敗になってしまうので、DはEに勝った。
ここで、DがEに負けてしまうと、2チームとも3勝2敗になってしまうので、DはEに勝った。 ここで、AがCに勝つと、AもCも2勝3敗になるので、AはCに負けた。
ここで、AがCに勝つと、AもCも2勝3敗になるので、AはCに負けた。 よって、正解は、肢①です。2つのパターンを知っていれば、そんなに難しくはない問題です。
よって、正解は、肢①です。2つのパターンを知っていれば、そんなに難しくはない問題です。