3日前は、国税専門官の本試験が行われ、昨日京都校に行くと、質問攻めにあいました。 それにしても、テレビのチャンネルのやつは難問でしたねえ。あんなのは、捨て問題だと思いますよ。 さて、その中から1問。no22です。 図のように、縦6行、横10列で60枚のラベルが並んだシートがたくさん用意されている。これらのシートのラベルに、次のルールで数字を印字する作業を行うこととする。 ［ルール］ ①各シートにおいて、一番右側の列にあるラベルに上から順に数字を印字し、印字し終えたら、一つ左側の列にあるラベルに上から順に数字を印字する。（図の矢印） ② ①を繰り返し、一番左側の列にある全てのラベルに数字を印字し終えたら、次のシートに取り替えて、同様に印字する。 ③数字は、1、2、…、44の44個の整数とする。また、値の小さい方から順に印字し、44の次は再び1に戻る。 ところが、5枚目のシートにある全てのラベルに印字し終えた段階で数字を確認したところ、それまでの作業は③ではなく次の③’に基づいていることが分かった。 ③’数字は、1、2、…、45の45個の整数とする。また、値の小さい方から順に印字し、45の次は再び1に戻る。 そこで、6枚目以降のシートは、①、②、③に基づいて、改めて、シートの一番右上のラベル（一番右側の列にあるラベルで一番上にあるもの）に印字する数字を1として、印字を行い、シートの一番左下のラベル（一番左側の列にあるラベルで一番下にあるもの）に初めて44が印字された時点で、作業を終えた。作業を終えた時点で、44が印字されたラベルの枚数は、1～5枚目のシートにある44が印字されたラベルも含めて全部で何枚か。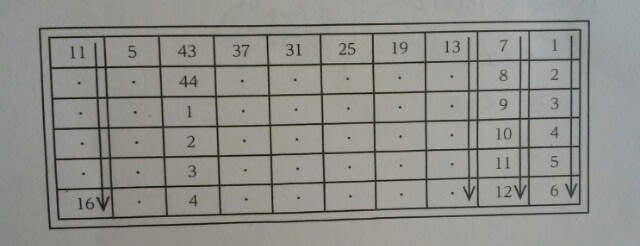
①17枚②21枚③25枚④29枚⑤33枚 かなり長文ですが、要するに、「5枚目まで作業をしたら、ちょびっとミスってたことに気づいたので、6枚目以降はミスらずにやりましたよ」ということですね。（このちょびっとがポイント） 1枚のシートには、60個印字するので、5枚作業をすると、60×5＝300個印字します。 このとき、③のルールを守っていれば、300÷44＝6余り36なので、「44」は、6回印字され、5枚目の左下には36という数字が印字されていたはずです。 繰り返しますが、ここがポイントです。 「では、いつルール③からルール③’になったの？」とか、「5枚目の左下の数字は何？」ということが気になりますが、正解は、「いつでも、そして何番でもよろしい」です。ルール③とルール③’では、数字は1しか違わないからです。（ただし、最後が1とか2付近でで終わるはずだった場合は、よく調べてみないといけませんが） ここまでまとめますと、 ★5枚目までに「44」は、6回印字されている。 ★いつ③から③’になったとしても、「44」が6回印字されていることには変わりがない ★もっと言えば、選択肢を見れば、1枚くらいずれたとしても、十分正解の選択肢は見つかる。ということです。 さて、6枚目以降です。 1枚のシートには60箇所印字する場所があって、、印字は44までで1セットだから、60と44の最小公倍数を計算して、660。
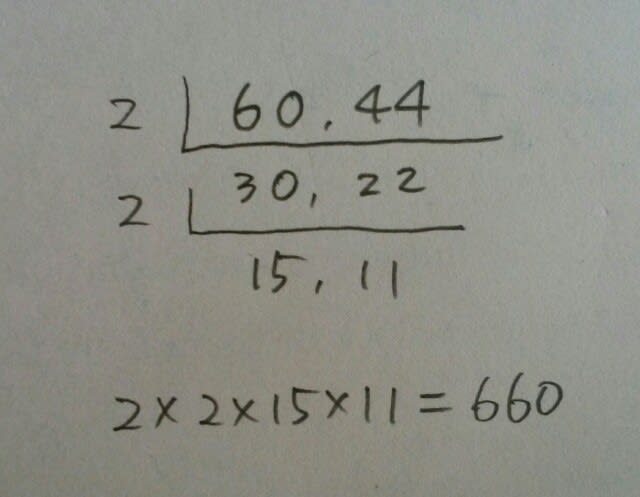660÷44＝15。6枚目以降には、「44」は、15枚あります。よって、1から5枚目のシートには6枚、6枚目以降には15枚、合わせて21枚。正解は、肢②です。 本問は、いつルールが切り替わっても、それは正解とは関係ない！気にするなよ！ということでしたが、これに似た問題、国家公務員ではたまに見かけます。地方公務員ではほとんど無かったと思います。それでも気になる気になる！という人は、以下を参照して下さい。
やはり、5枚目の左下の数字が1ずつ変化するだけで、どっちみち「44」が6枚であることが分かりますね。そして、たとえこれが実は5枚になったり7枚になったりするとしても、選択肢を見ると、1枚くらい事実と違っていても、正解の選択肢は選べるという状況になっていますね。ここをポチッとお願いします。→
にほんブログ村
①17枚②21枚③25枚④29枚⑤33枚 かなり長文ですが、要するに、「5枚目まで作業をしたら、ちょびっとミスってたことに気づいたので、6枚目以降はミスらずにやりましたよ」ということですね。（このちょびっとがポイント） 1枚のシートには、60個印字するので、5枚作業をすると、60×5＝300個印字します。 このとき、③のルールを守っていれば、300÷44＝6余り36なので、「44」は、6回印字され、5枚目の左下には36という数字が印字されていたはずです。 繰り返しますが、ここがポイントです。 「では、いつルール③からルール③’になったの？」とか、「5枚目の左下の数字は何？」ということが気になりますが、正解は、「いつでも、そして何番でもよろしい」です。ルール③とルール③’では、数字は1しか違わないからです。（ただし、最後が1とか2付近でで終わるはずだった場合は、よく調べてみないといけませんが） ここまでまとめますと、 ★5枚目までに「44」は、6回印字されている。 ★いつ③から③’になったとしても、「44」が6回印字されていることには変わりがない ★もっと言えば、選択肢を見れば、1枚くらいずれたとしても、十分正解の選択肢は見つかる。ということです。 さて、6枚目以降です。 1枚のシートには60箇所印字する場所があって、、印字は44までで1セットだから、60と44の最小公倍数を計算して、660。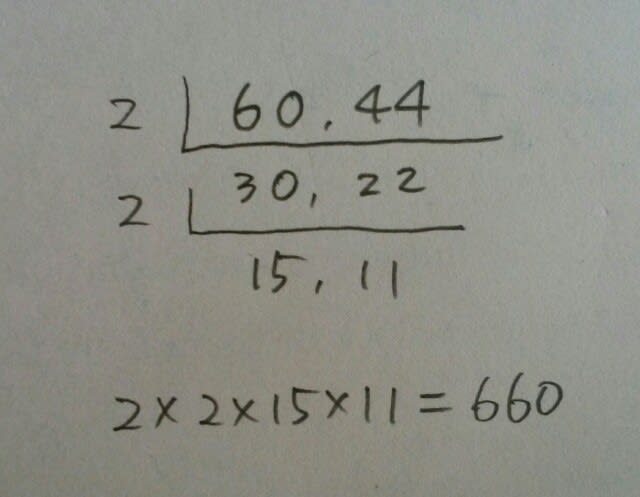660÷44＝15。6枚目以降には、「44」は、15枚あります。よって、1から5枚目のシートには6枚、6枚目以降には15枚、合わせて21枚。正解は、肢②です。 本問は、いつルールが切り替わっても、それは正解とは関係ない！気にするなよ！ということでしたが、これに似た問題、国家公務員ではたまに見かけます。地方公務員ではほとんど無かったと思います。それでも気になる気になる！という人は、以下を参照して下さい。やはり、5枚目の左下の数字が1ずつ変化するだけで、どっちみち「44」が6枚であることが分かりますね。そして、たとえこれが実は5枚になったり7枚になったりするとしても、選択肢を見ると、1枚くらい事実と違っていても、正解の選択肢は選べるという状況になっていますね。ここをポチッとお願いします。→
にほんブログ村
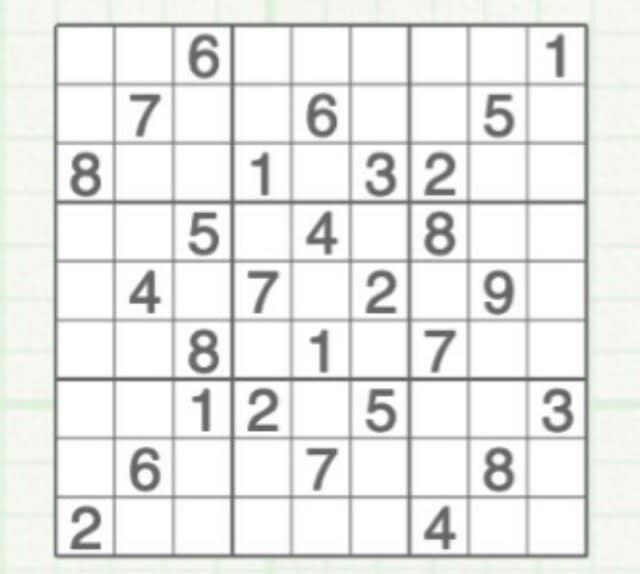縦と横に1から9までの数字を重複しないように書き込んでいきます。なおかつ、太い四角で囲まれたところも、1から9を重複しないようにして完成させます。ほんのちょっとミスると、おかしくなって、はじめからやり直し。完成したときには、達成感が半端じゃありません。初級から上級まで、種類も豊富！公務員試験を受ける人は、絶対にやるべきですよ。何故かは、今日の記事を読むと分かります。 先日の警視庁no35より。 A～Fの6人が総当たり戦でテニスの試合を行った。各人とも毎日1試合行い、5日間で全試合が終了した。次のことが分かっているとき、Fが1日目に対戦した相手として、最も妥当なのはどれか。 ・AとBは3日目に対戦した。 ・BとEは2日目に対戦した。 ・CとDは4日目に対戦した。 ・DとEは5日目に対戦した。 ①A②B③C④D⑤E まずは、総当たり戦の表を書きます。
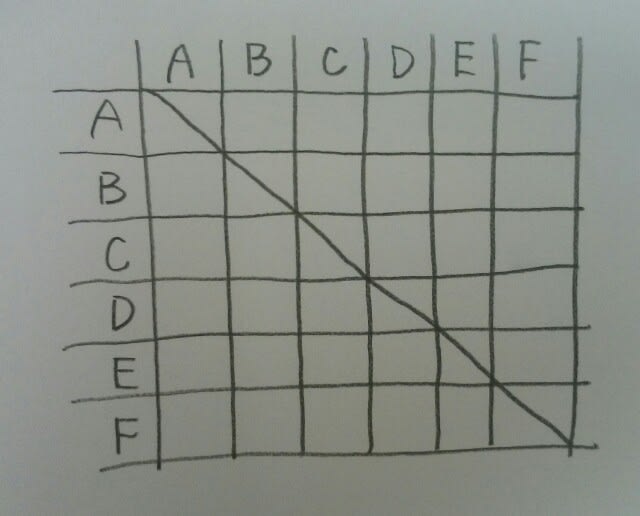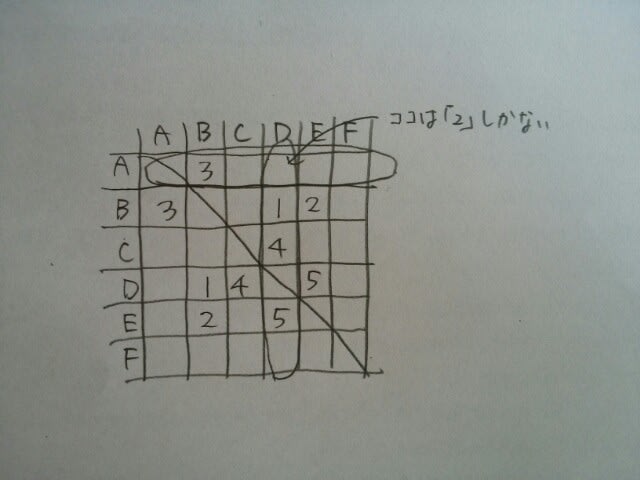
この表には、勝ち負けを記入するのではなく、その試合が何日目だったかという数字を記入します。4つの条件を記入すると、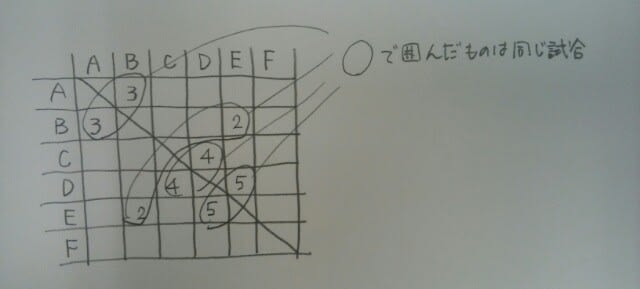
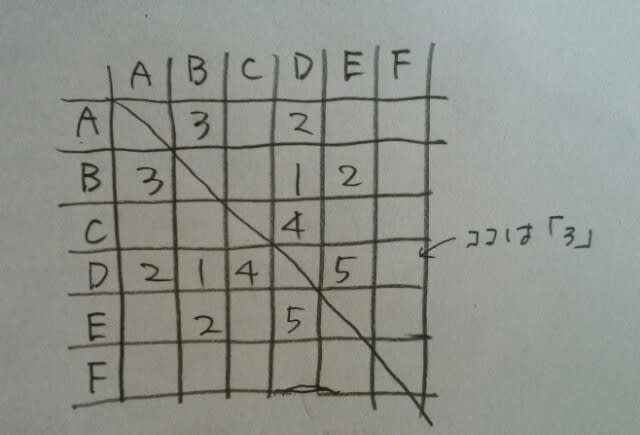
各人とも毎日1試合を行ったので、この表を横に見ても縦に見ても、1、2、3、4、5が一つずつ入ることになります。例えば、「2」が重複していたら、その人は2日目に2試合以上することになるからです。また、「2」がないならば、その人は2日目に試合をしないことになってしまいます。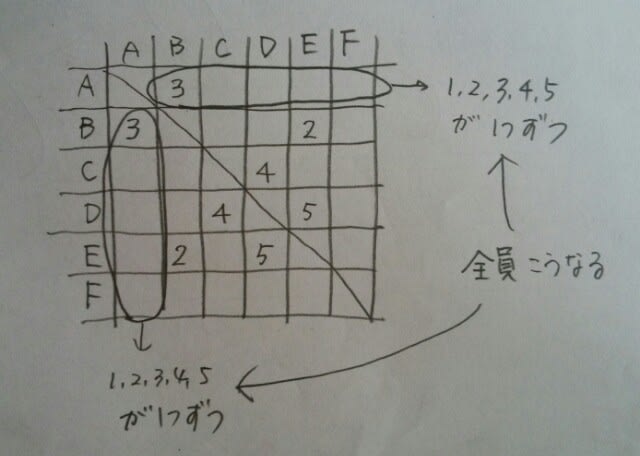
さあ、それでは、このパズルを完成して下さい。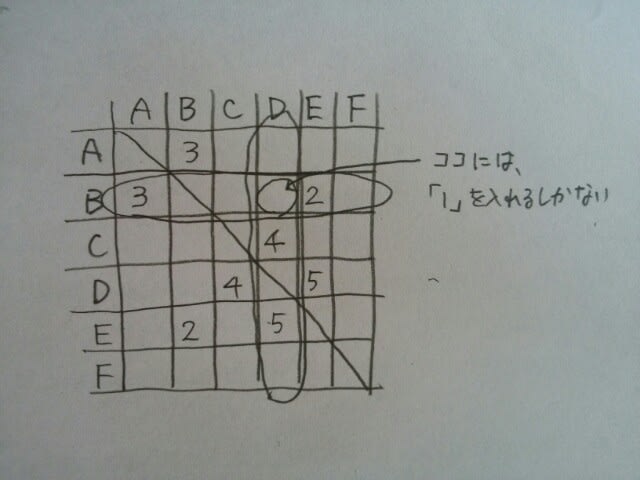
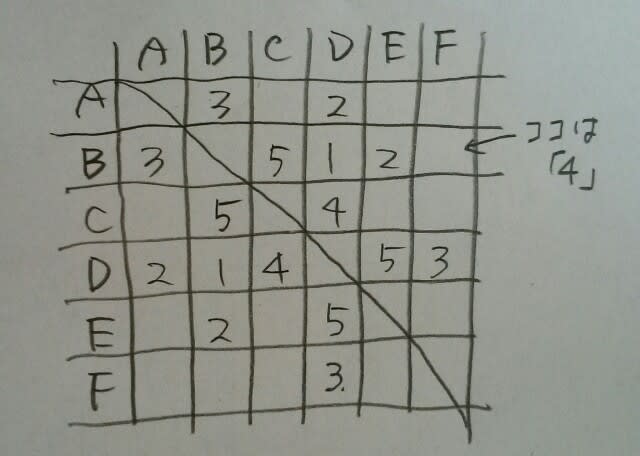
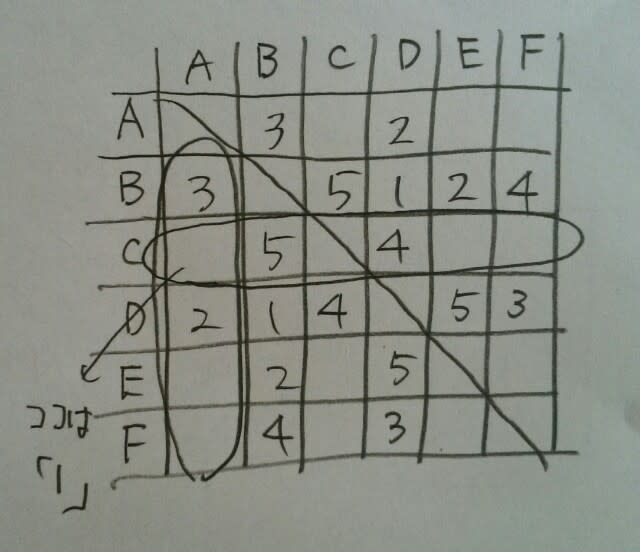もうこの先は大丈夫ですね。こうなります。
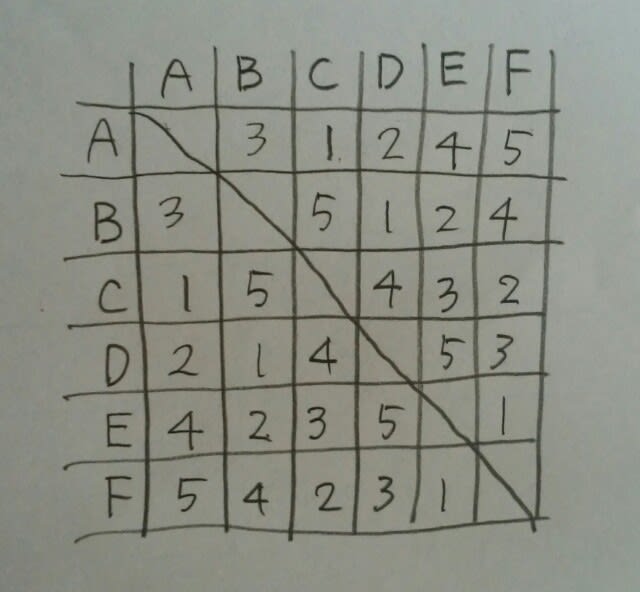Fは、1日目にEと対戦しています。正解は、肢⑤です。 数独の場合は、縦横に1～9を重複せずに入れるだけではなく、太い枠内にも重複せずに1～9を入れなくてはならず、この問題の数倍難しくなっています。数独を少しでもやったことがあれば、本問は易しかったはずだし、そんなのやったことないという人にとっては難しく感じるのかもしれません。 少し自慢します。このブログの2017年5月26日「練習問題①（平成22年警察官）」の記事で、ほとんど同じ問題を扱っています。的中です。こんなにいっぱい記事があれば当たり前ですが……。 何日目の対戦？という問題は、全て十字パズルで解決できるとは限りません。参考書などに載っている、別解も大事ですので、本気で公務員試験に臨む方は、合わせて勉強して下さい。 さて、練習のために、はじめの数独を完成させてみて下さい。正解は、こうです。
ここをポチッとお願いします。→
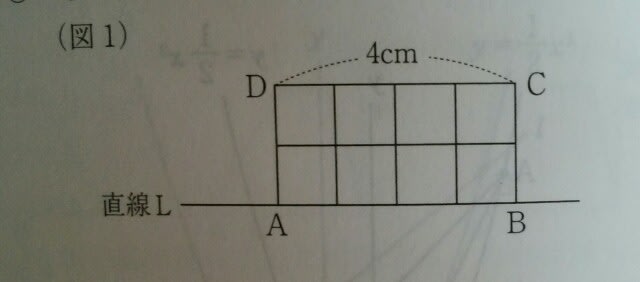
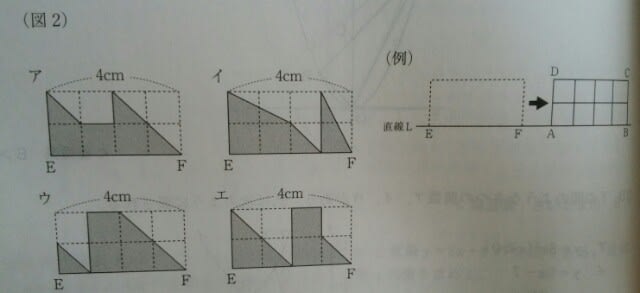
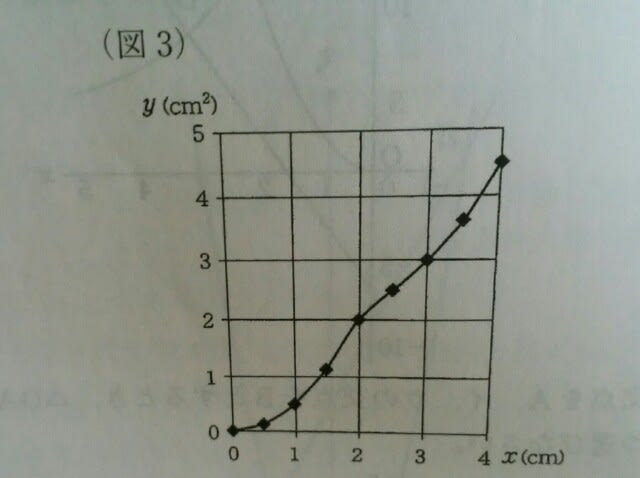①ア ②イ ③ウ ④エ xが2～3になったときに、yが1㎠増加しているので、正解は、①です。 図2の色がぬられた部分を、「幸せ」と考えてみて下さい。そして、図1は、あなたの心の中です。はじめ、あなたの心の中は、幸せが全くありません。でも、図2のいずれかがあなたの心に近づき、やがてはあなたの心の中に幸せを連れて入ってきてくれるのです。そう、図3は、あなたの「幸せグラフ」なのです。（今日はロマンチック～。）例えば、アの場合、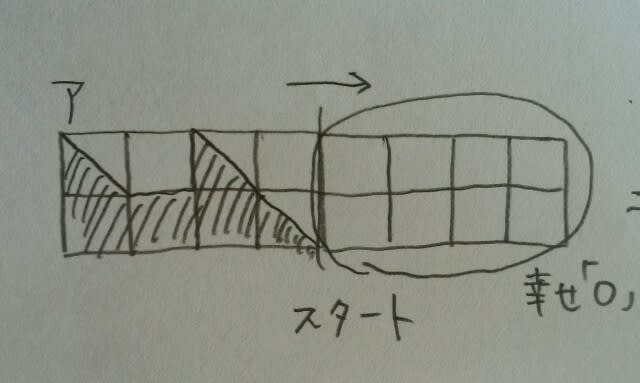
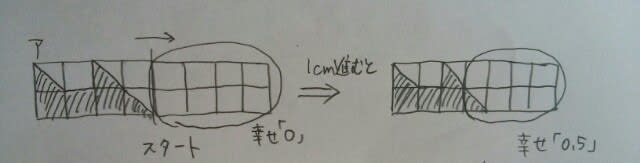
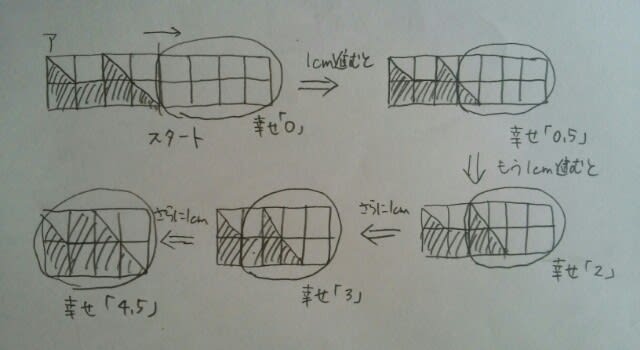幸せグラフとぴったり一致しています。 イの場合は、1cm進むと幸せはいきなり1になるので、グラフと一致していません。ウの場合、3cm進むと幸せは4になり、一致しません。エの場合は、2cm進むと幸せは2.5で、これも一致しません。結局、正解まで最短でたどり着くには、
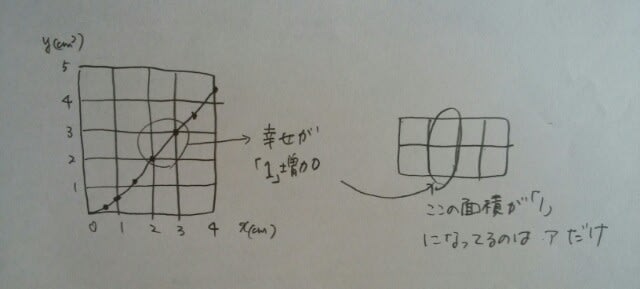などとやれば良いでしょう。 ここから先は応用編になりますが、例えば、xが0～1のときは2次関数（曲線）なのに、xが2～3のときは1次関数（直線）になっていますね。これはどういうことでしょう？
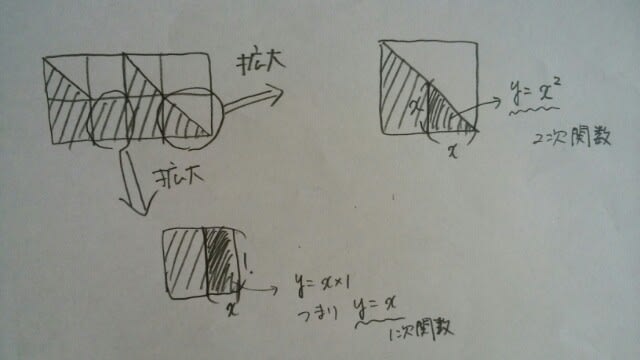ということでしたね。xが1～2、3～4も同様で、
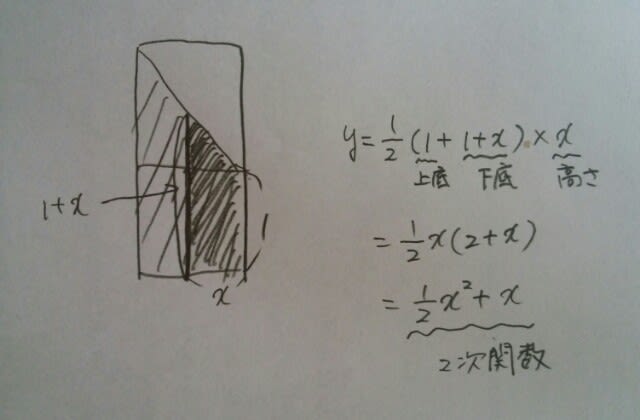です。正解は、肢①でした。ここをポチッとお願いします。→