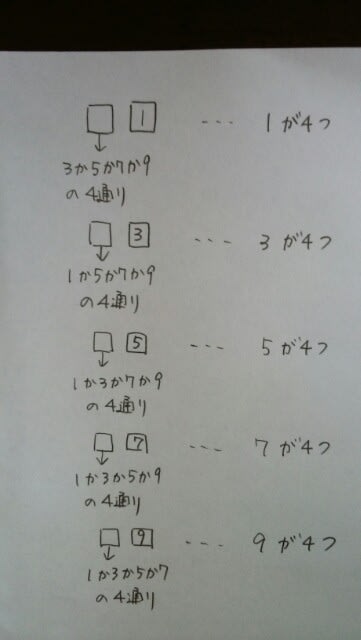
1、3、5、7、9の5つの数字から、異なる2つを選んで任意の2桁の整数を作る。できた2桁の整数の総和として、最も妥当なのはどれか。①1100②1221③1321④1360⑤1469 2桁の整数は、何個できるかというと、5×4＝20個ですから、これを全部足せば答えは出ます。実は、これがとても大事なことになってきます。
例えば、257＋670＋344を、筆算でやってみます。
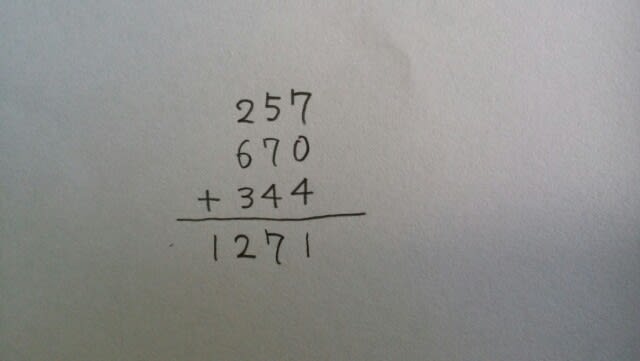まず、1の位の数だけ足しまして、7＋0＋4＝11。このとき、10の位や、100の位の数を見ましたか？見なかったですね。次に、10の位の数だけを足しまして、5＋7＋4＝16。ただし、1の位を足したときに1繰り上がってたので、16＋1＝17。このとき、1の位や100の位の数は見ていません。最後に100の位の数を足しまして、2＋6＋3＝11。ただし、10の位を足したときに、1繰り上がってたので、11＋1＝12と、計算しますね。つまり、
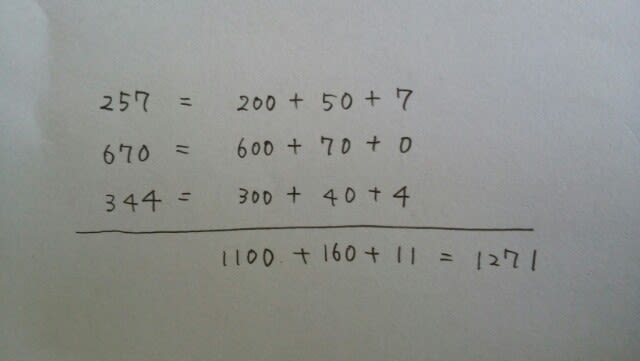ということです。100の位だけ足して、10の位だけ足して、1の位だけ足して、合わせる。本問の場合は、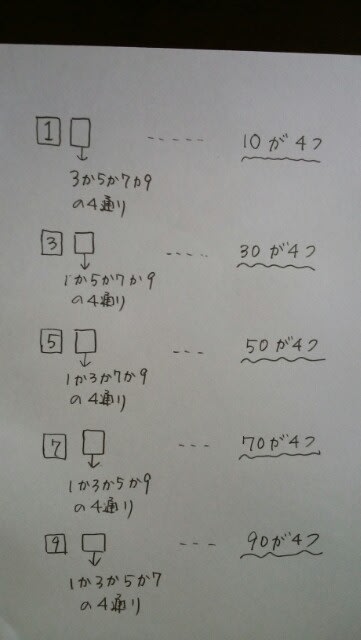
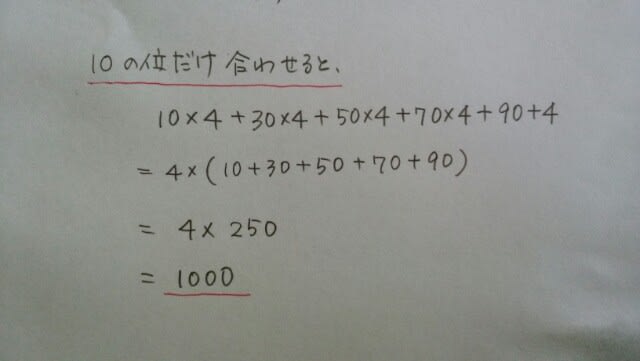
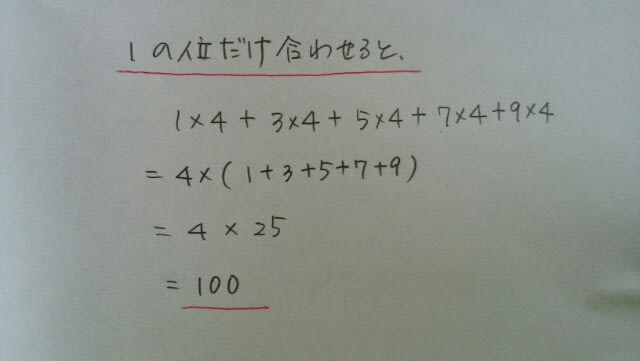よって、1000＋100＝1100。正解は肢①です。結局、10の位の和が1000ならば、1の位の和は、1000を、一桁小さくした100になっていますね。3桁や、4桁になった類題も、1番大きな位だけ真面目に計算しておいて、後は一桁ずつ小さくしたものを足せばOKです。
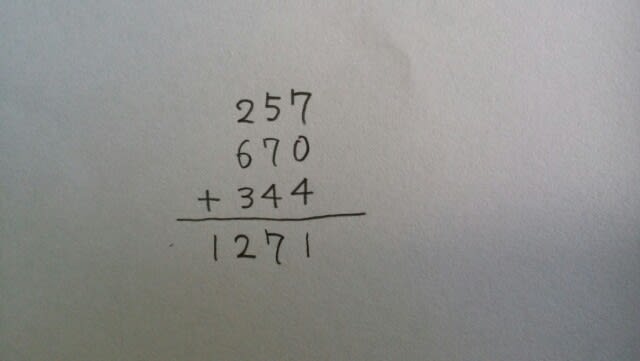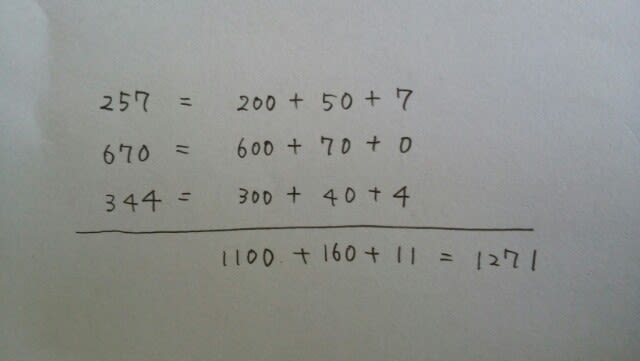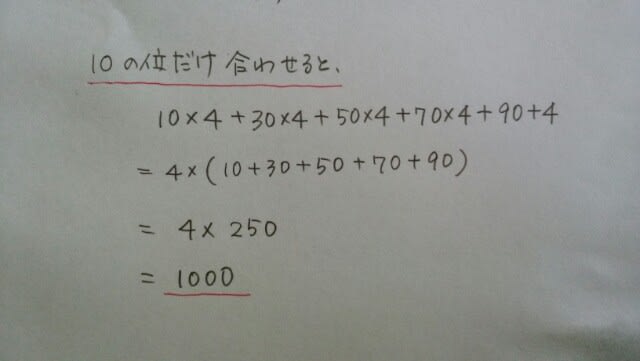
例えば、257＋670＋344を、筆算でやってみます。まず、1の位の数だけ足しまして、7＋0＋4＝11。このとき、10の位や、100の位の数を見ましたか？見なかったですね。次に、10の位の数だけを足しまして、5＋7＋4＝16。ただし、1の位を足したときに1繰り上がってたので、16＋1＝17。このとき、1の位や100の位の数は見ていません。最後に100の位の数を足しまして、2＋6＋3＝11。ただし、10の位を足したときに、1繰り上がってたので、11＋1＝12と、計算しますね。つまり、ということです。100の位だけ足して、10の位だけ足して、1の位だけ足して、合わせる。本問の場合は、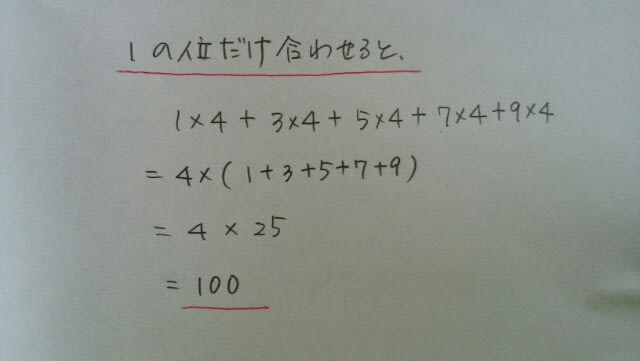よって、1000＋100＝1100。正解は肢①です。結局、10の位の和が1000ならば、1の位の和は、1000を、一桁小さくした100になっていますね。3桁や、4桁になった類題も、1番大きな位だけ真面目に計算しておいて、後は一桁ずつ小さくしたものを足せばOKです。
2つとも、非常に大事なことで、実は、小学校の3年生で学習していたのです。特に、②は、うっかり確認を怠ることがよくあります。15÷7＝1余り8などとしてはいけませんね。本問の場合は、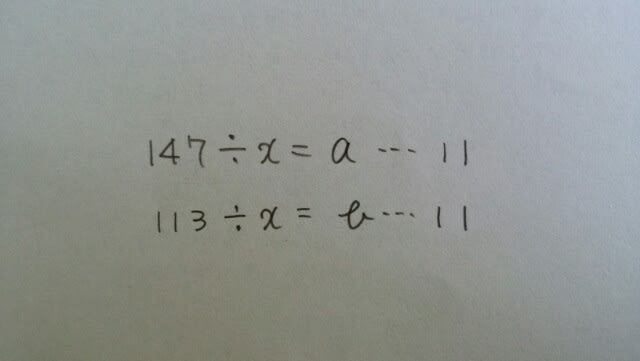
ということですから、
ところで、約数とは？例えば、20の正の約数をすべてみつけましょう。
□や、○に入るものが、20の約数です。
よって、20の正の約数は、1、2、4、5、10、20です。
ということで、xは、136と102の公約数です。では、公約数ってどうやって求めるの？公約数を、全て求めるときは、まず最大公約数を求め、その最大公約数の約数を求めればいいのです。136と102の最大公約数は、
34ですから、その34の約数を求めます。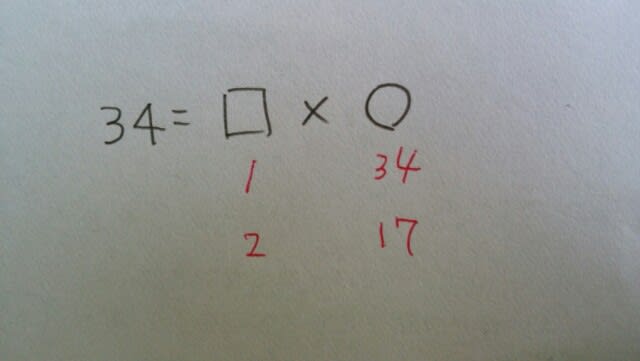
1、2、17、34です。しかし、割る数は、余りよりも大きくなければいけません（割る数＞余り） xは、11よりも大きくなければいけないので、17か、34です。17だつたとすると、15で割ると余りは2。これは選択肢にはありません。34だつたとすると、15で割ると余りが4。これは肢②にあります。よって、正解は肢②です。
Nが最小となるのは、mが1のときなので、N＝56×1－3＝53。53÷9＝5余り8。正解は、肢①です。実は、剰余の問題には、もう一つあります。～で割ると～余る。ではなく、～を割ると～余る。というやつです。それはまた、これとは似ていますが、少し違ってきますので、次回説明します。
今回は、その③。 次の問題は、地方初級（社会人）の過去問です。 4で割ると1余り、9で割ると3余るような2桁の自然数はいくつあるか。①1個②2個③3個④4個⑤5個 この場合は、N＝4a＋1＝9b＋3と立式しても、うまくまとまりません。とにかく、根性で、1つ見つけます。 4で割ると1余る自然数を、どんどん書き出します。その次に、9で割ると3余る自然数をどんどん書き出します。
共通するものはないかな？と、眺めてみると、
図に書いておきましたが、上の段は、4ずつ増加。下の段は、9ずつ増加しているので、初めに出てきた21から、36（4と9の最小公倍数）進むと、また共通する数が現れます。さらに36進むと、再び共通する数が現れますね。式で表すと、21＋36m（mは整数）となります。2桁という条件を満たすものは、m＝0（このときは21）、m＝1（このときは57）、m＝2（このときは93）の3個。よって、正解は肢③です。その1に書いていますが、もう一度繰り返すと、こうなるのです。
次回、東京消防庁1類の過去問を紹介します。
今回は、②について。 次の問題は、警察官（大卒）の過去問です。 ある3桁の整数を7、8、9で割ると、余りはそれぞれ6、7、8となる。この3桁の整数のそれぞれの位の和はいくらか。①6②8③10④12⑤14 ある整数をNとします。Nは、7で割ると6余るので、N＝7a＋6。同様に、8で割ると7余るので、N＝8b＋7。9で割ると8余るので、N＝9c＋8。まとめると、
ここで、次のことに注目します。
全部差が同じ数（この場合は1）になっています。この場合は、それぞれの辺に、その同じ数（この場合は1）を足します。
N＋1は、7の倍数かつ8の倍数かつ9の倍数ですから、504の倍数です。
よって、5＋0＋3＝8。正解は肢②です。なぜこうなるのかというと、7で割ると6余るということは、その数が、あと1だけ大きかったら、うまく7で割り切れたのに、ちょっと残念！8で割ると7余るということは、その数が、あと1だけ大きかったら、8で割り切れたのに、ちょっと残念！……ということです。次回で、パターン③を説明します。