Aで割るとB余る。とか、A人ずつイスに座ると最後のイスにB人座ることになった。とか、ミカンをA個ずつ袋に入れていったら、B個余ったとかいう問題を、剰余の問題といいます。 行き当たりばったりで考えるのではなく、3つのパターンを覚えておいて、どのパターンかを見抜いた上で解きましょう。
簡単にまとめると、やり方はこうです。①引いて余りを消せ！②足して余りを消せ！③書き出せ！ 一番よく出題されるのは、②のパターンです。 とりあえず今回は、①について説明します。これは、地方初級の過去問です。 2、3、7のいずれで割っても1余る整数のうち、10以上2000以下のものは何個あるか。
題意を満たす整数をNとします。Nは、2で割ると1余るので、2a＋1（aは整数）と書きあらわすことができます。同様に、3で割ると1余るので、3b＋1、7で割ると1余るので、3c＋1とも書きあらわすことができます。
これが、引いて余りを消せ！のことです。さて、N－1は、2の倍数でもあり、3の倍数でもあり、7の倍数でもあるのだから、42の倍数です。（最小公倍数）
ということで、正解は肢②です。次回で、パターン②を説明します。
にほんブログ村
簡単にまとめると、やり方はこうです。①引いて余りを消せ！②足して余りを消せ！③書き出せ！ 一番よく出題されるのは、②のパターンです。 とりあえず今回は、①について説明します。これは、地方初級の過去問です。 2、3、7のいずれで割っても1余る整数のうち、10以上2000以下のものは何個あるか。題意を満たす整数をNとします。Nは、2で割ると1余るので、2a＋1（aは整数）と書きあらわすことができます。同様に、3で割ると1余るので、3b＋1、7で割ると1余るので、3c＋1とも書きあらわすことができます。これが、引いて余りを消せ！のことです。さて、N－1は、2の倍数でもあり、3の倍数でもあり、7の倍数でもあるのだから、42の倍数です。（最小公倍数）ということで、正解は肢②です。次回で、パターン②を説明します。
にほんブログ村
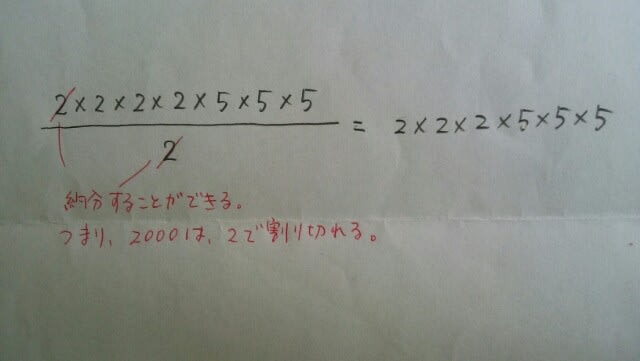2000は、2で割り切れるからです。
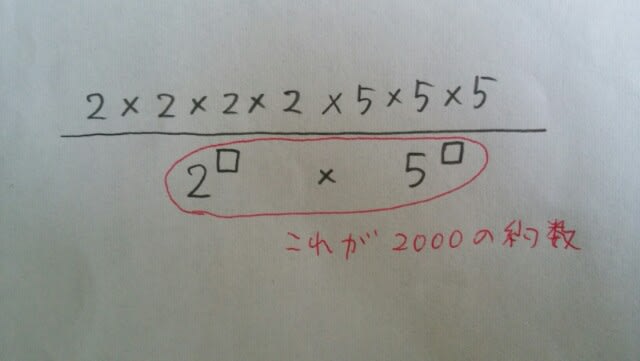どんな数字でも、0乗すると、1です。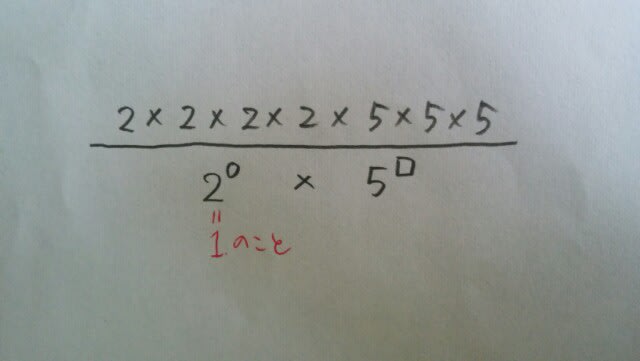
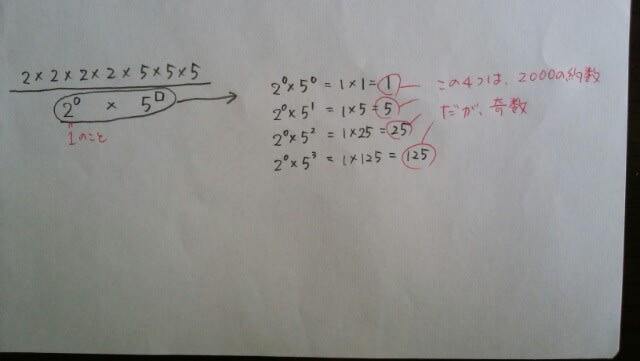本問は、約数のうち、偶数は何個あるか？です。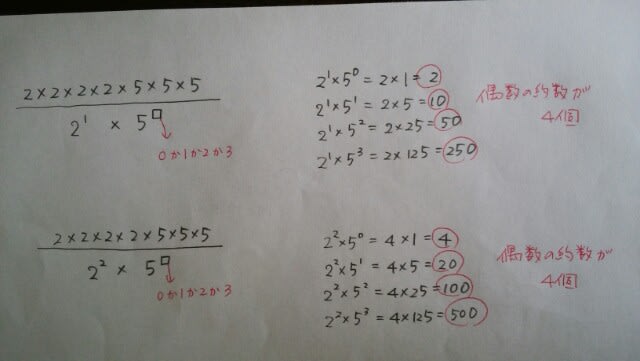
よって、4×4＝16個あります。正解は肢②です。分かっている人にとっては、少しくどかったと思います。結局、まとめてみると、
まず、5の倍数の和は、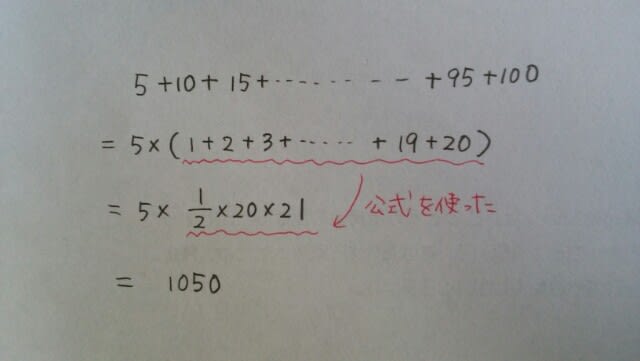
同様に、7の倍数の和は、
だからといって、1050＋735＝1785が正解というわけではありません。「5の倍数及び7の倍数のうち共通する数」すなわち35の倍数を、重複して足しているからです。1から100までの自然数で、35の倍数は、35と70の2個です。よって、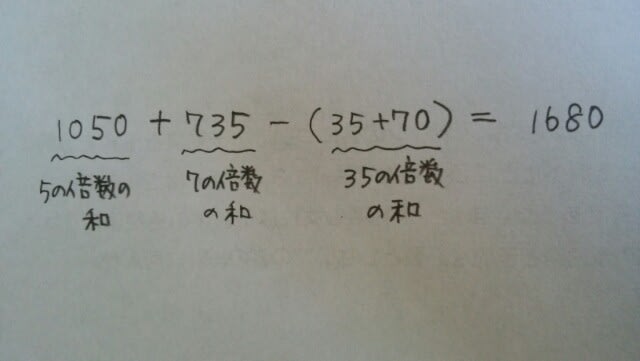
正解は肢⑤です。
①14②16③18④20⑤22 ②の、引き算は、足し算に直しておくほうが良いとおもいます。
正解は②でした。
正解は⑤です。