図のように、合同な4つの正三角形を、三角形の辺どうしがぴったり合うように並べるとき、次の問いに答えなさい。ただし、回転したり裏返したりして、ぴったり重なる図形は1種類とする。 (1) できる図形は何種類あるか、求めなさい。 (2) 線対称な図形は何種類あるか、求めなさい。 (3) 線対称な図形について、対称の軸を軸として1回転させてできる立体を考える。そのうち最も大きい体積は、何立方センチメートルか求めなさい。ただし、正三角形の1辺の長さを2cmとし、円周率はπとして計算しなさい。 (1) 合同な正三角形が2つあったとします。
3つあったとします。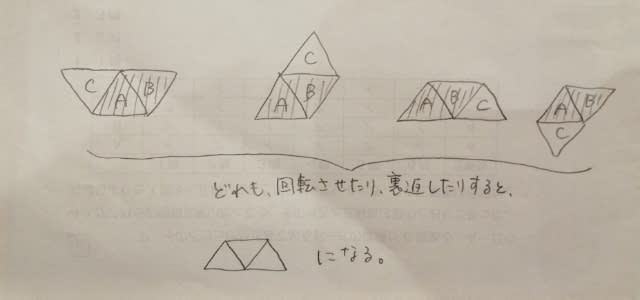
結局、合同な正三角形が3つあって、辺どうしがぴったり合うように並べると、どうやったって、1種類しかできないのです。 では、もう一つ増やすとどうなるの?というのが本問の趣旨です。やってみましょう。
正解は、3種類です。 こういうのが苦手な人には、酷かもしれませんが、もしも本問が、「回転させてもよいが、裏返してはいけない」という条件であれば、①は、回転させても③にはならず、④は、回転させても裏返しても⑤になるので、正解は4種類となります。 (2)①③型は線対称ではなく、②型と④⑤型は線対称なので、正解は2種類です。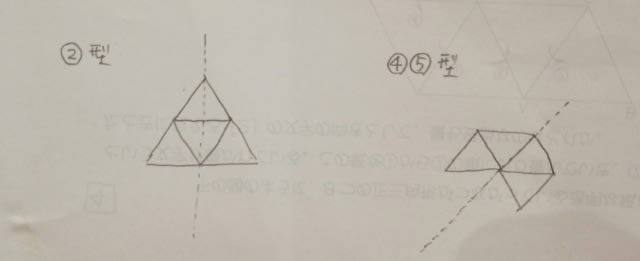
(3) まず、②型です。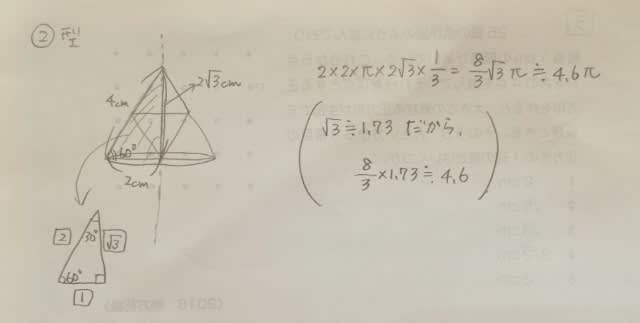
次に④⑤型です。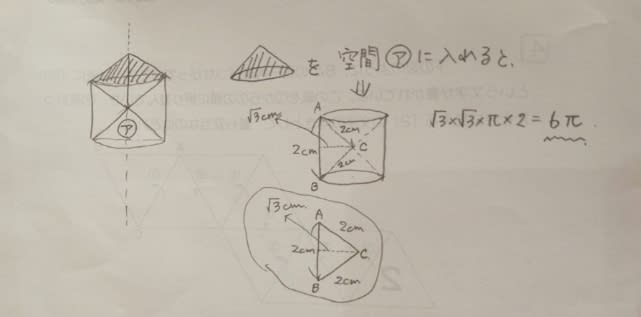
④⑤型の方が体積が大きく、6π立方センチメートルです。ここをポチッとお願いします。→
にほんブログ村


3つあったとします。

結局、合同な正三角形が3つあって、辺どうしがぴったり合うように並べると、どうやったって、1種類しかできないのです。 では、もう一つ増やすとどうなるの?というのが本問の趣旨です。やってみましょう。

正解は、3種類です。 こういうのが苦手な人には、酷かもしれませんが、もしも本問が、「回転させてもよいが、裏返してはいけない」という条件であれば、①は、回転させても③にはならず、④は、回転させても裏返しても⑤になるので、正解は4種類となります。 (2)①③型は線対称ではなく、②型と④⑤型は線対称なので、正解は2種類です。

(3) まず、②型です。
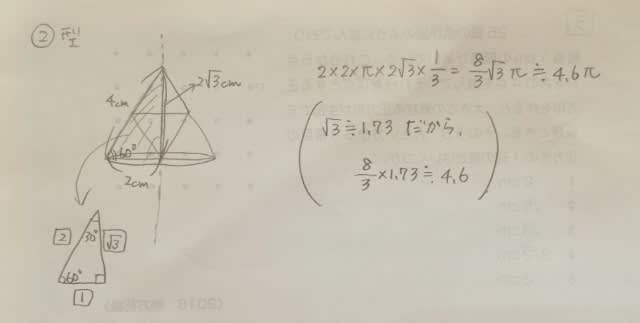
次に④⑤型です。

④⑤型の方が体積が大きく、6π立方センチメートルです。ここをポチッとお願いします。→
にほんブログ村
















