【裏技 食塩水の問題】(再掲)

濃度a％の食塩水Agと濃度b％の食塩水Bgを混ぜるとc％の食塩水Cgができた。ただし、a＜bとする。

A+B=C …① →食塩水

aA+bB=cC …② →食塩

上の連立方程式を解く。

①×b-② (b-a)A=(b-c)×C

A=((b-c)/(b-a))×C

②-①×a (b-a)B=(c-a)×C

B=((c-a)/(b-a))×C

上の関係を使って問題を解いてみよう。

例①)【混合】

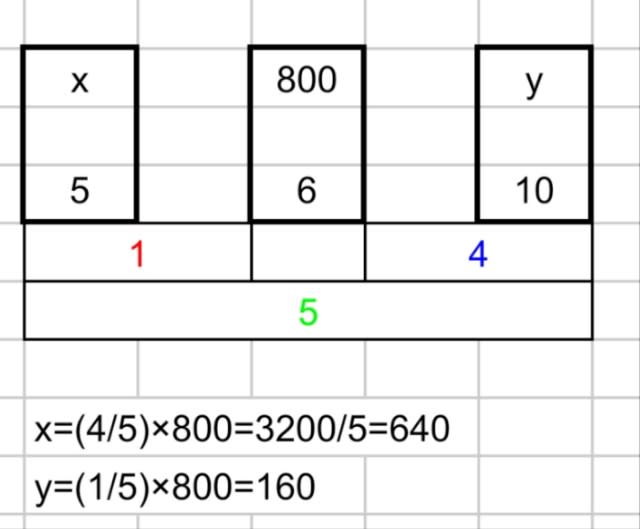
5%と10%の食塩水を混ぜ合わせて、6％の食塩水を800ｇ作りたい。

それぞれ何gずつ混ぜたらよいか求めなさい。

例②)【混合】

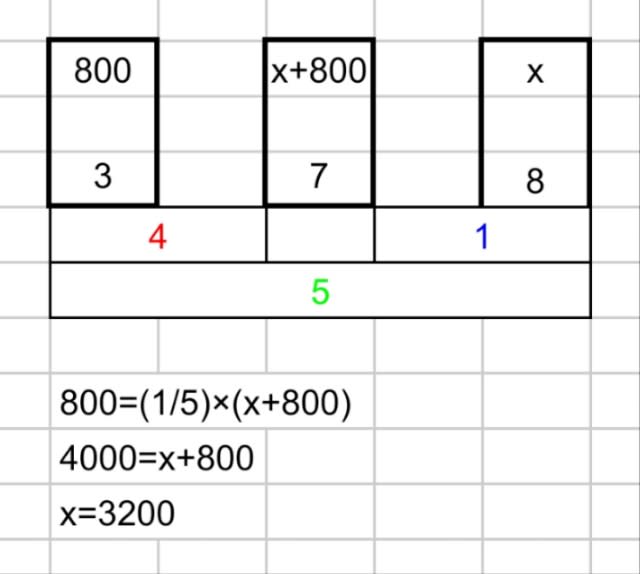
3%の食塩水800gに8%の食塩水を加えて、7%の食塩水にしたい。加える食塩水の量は何gか?

例③)【水の追加】

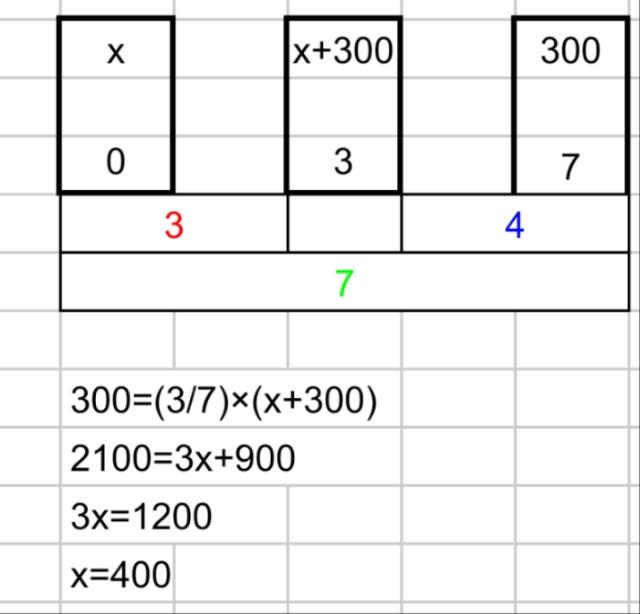
濃度が7%の食塩水300gがあります。その食塩水の濃度を3%にするには、何g水を足せばいいでしょうか？

(※水の濃度は0％とする)

例④)【水の蒸発】

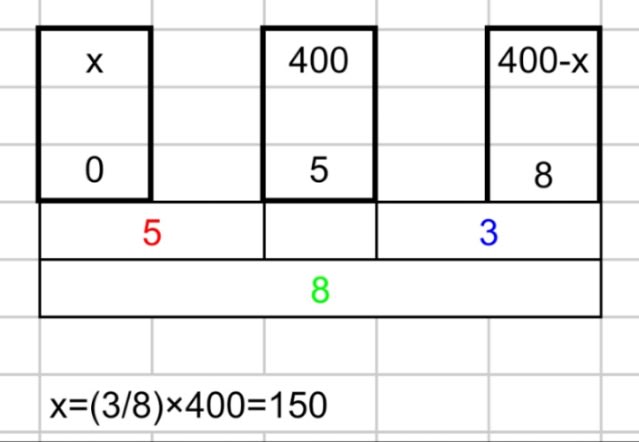
5％の食塩水400gからに水を蒸発させると、8％の食塩水になった。蒸発した水は何gか。

(8％の食塩水に蒸発した水を加えると5％の食塩水400gになる。)

(※水の濃度は0％とする)

例⑤)【食塩の追加】

濃度が20%の食塩水600gがあります。その食塩水の濃度を25%にするには、何g食塩を足せばいいでしょうか？

(※食塩の濃度は100％とする)

例⑥)【混合】

5％の食塩水300gに200gの食塩水を加えて混ぜると、7％になった。加えた食塩水の濃度はいくらか？

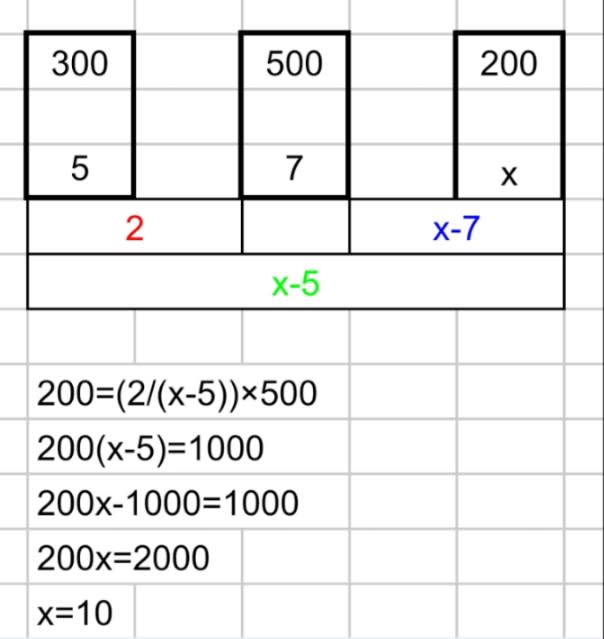
連立方程式を解いた方が早いが、視覚的に面白いと思った。また、混合、水の追加、水の蒸発、食塩の追加の問題が一通りの方法で解けるのも面白い。

以前発表したものだが、視覚的に分かりにくいので再掲した。

(2024/3/30)

期待値

1~7の数字がそれぞれ書かれたカードが7枚ある。このカードを無作為に2枚取るとき、1枚目のカードをA、2枚目のカードをBとする。

(1)x=A×Bの期待値を求めよ。

(2)y=A/Bの期待値を求めよ。

今日の？【2024/3/24】(ロシアテロに思う)

2024年3月22日にロシアの首都モスクワ郊外のコンサートホールで起きたテロ事件では、これまでに133人が死亡しました。プーチン大統領は、国民向けのビデオ演説で実行犯とみられる4人を含めて11人の容疑者を拘束したとしたうえで「事件に関与した全員を処罰する」と強調しました。(2024/3/24)

テロで亡くなられた方の冥福を祈る。

また、怪我をされた方の早い回復を祈る。

プーチン大統領は、ウクライナで亡くなられた方や怪我をされた方に対してどのように感じているのだろか？

ウクライナで行われている行為はテロと同じである。テロが決して許されないように、戦争も決して許してはいけない行為なのだ。

テロに加担した者を処罰するのであれば、戦争に加担した者も処罰しなければなるまい。

【x^2=a+biを解く】

a,bの少なくとも一方は整数とし、kを自然数とし、a^2+b^2=k^2とする。

このとき、x^2=a+biを解く。

a+bi=p(cosα+isinα)とする。

p=√(a^2+b^2)=k, cosα=a/p, sinα=b/p

x=c+di=r(cosθ+isinθ)とする。

c=rcosθ, d=rsinθ

x^2

=r^2(cos2θ+isin2θ)=p(cosα+sinα)

よって、

r^2=p

cos2θ=cosα→2(cosθ)^2-1=a/p

sin2θ=sinα→2sinθcosθ=b/p

2(rcosθ)^2-p=a

2c^2=a+p

c^2=(a+p)/2→c^2=(a+√(a^2+b^2))/2

2(rsinθ)(rcosθ)=b

2cd=b

【例】x^2=5+12i

p^2=5^2+12^2=169→p=13

c^2=(5+13)/2=9→c=±3

6d=12→d=2

よって、

x=±(3+2i)

【例】x^2=3-4i

p^2=3^2+(-4)^2=25→p=5

c^2=(3+5)/2=4→c=±2

4d=-4→d=-1

よって、

x=±(2-i)

【例】x^2=2+√5i

p^2=2^2+(√5)^2=9→p=3

c^2=(2+3)/2=5/2→c=±√5/√2=±√10/2

√10d=√5→d=1/√2=√2/2

よって、

x=±(√10+√2i)/2

【例】x^2=√7+3i

p^2=(√7)^2+3^2=16→p=4

c^2=(√7+4)/2→c=±√(4+√7)/√2

√(4+√7)=(√7+1)/√2だから

c=±(√7+1)/2

(√7+1)d=3→d=3/(√7+1)=3(√7-1)/6

=(√7-1)/2

よって、

x=±{(√7+1)/2+{(√7-1)/2}i}

※a,b共に整数でないときやa^2+b^2=k^2

でないときは、cは外れない二重根号になる。

(2024/3/18)

連立方程式

c^2-d^2=a

2cd=b

(c+di)^2=(c^2-d^2)+2cdi=a+bi

x^2=a+biを解くことになる。

【例】連立方程式

c^2-d^2=5

2cd=√11

【解】

x^2=5+√11i

p^2=5^2+(√11)^2=36→p=6

c^2=(5+6)/2=11/2→c=±√22/2

√22d=√11→d=√2/2

よって、

x=±{√22/2+(√2/2)i}

したがって、

(c,d)=(√22/2, √2/2)(-√22/2, -√2/2)

(2024/3/19)

今日の？【2024/3/21】(処分？)

自民党派閥の政治資金問題を巡る安倍派（清和政策研究会）幹部らへの党処分として、「選挙での非公認」を科す案が浮上した。これらの幹部以外で、政治資金収支報告書に不記載があった議員は「戒告」にとどめる案がある。

「戒告」は自民党内での処分で、国会議員としての責任の取り方でない。

「選挙での非公認」もそうだし、同じ選挙区内に自民党候補を立てず自主投票にすれば、「隠れ公認」になる。

自民党内の処分を4月上旬に予定しているようだが、全容が全くできていないのに、「蜥蜴の尻尾切り」になれなければよいのだが。

p.s.【戒告】言葉に出していましめること。

→怒られる間我慢すれば終わり？