【裏技-2元1次連立方程式の解法】

ax+by=p…①

cx+dy=q…②

①×d-②×b

(ad-bc)x=dp-bq→x=(-bq+dp)/(ad-bc)

①×c-②×a

(bc-ad)y=cp-aq→y=(-cp+aq)/(ad-bc)

【解法の手順】

(i)係数を抜き出す。

(p,qは符号を変える&a,cを右に追加)

a b -p a

c d -q c

(ii)左から順に2列抜き出し、2次の正方行列を考えその行列式を求める。

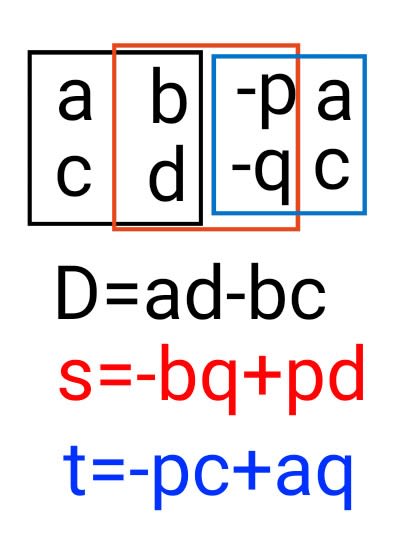
(iii)x=s/D, y=t/D

(※)

D=0のとき、

①=②×tとなるtが

存在する→不定(解は無数にある)

存在しない→解なし

(例1)

2x+3y=9

x+4y=7

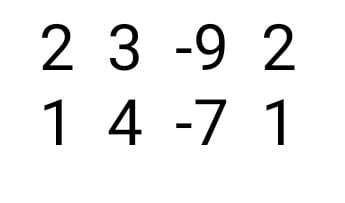D=2×4-3×1=8-3=5

s=3×(-7)-(-9)×4=-21+36=15

t=(-9)×1-2×(-7)=-9+14=5

よって、x=s/D=15/5=3, y=t/D=5/5=1

(例2)

4x-3y=1

3x+2y=-3

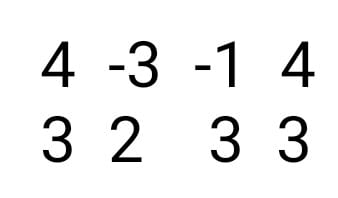
D=4×2-(-3)×3=8+9=17

s=(-3)×3-(-1)×2=-9+2=-7

t=(-1)×3-4×3=-3-12=-15

よって、x=-7/17, y=-15/17

(2020/10/27)

大人の数学教室105(数列④)

【第4章】

(4)等比数列

例11)2,6,18,54,162,…

隣り合った2 つの項に着目して、

比=(後ろの項)/(前の項) を考える。3,3,3,3 → すべての比が等しい

このように、隣り合った2 つの項の比がすべて等しい数列を「等比数列」といい、その比を「公比」という。

(後ろの項)=(前の項)×公比 だから、

初項と公比が決まれば、順々に項を作り、

等比数列を作ることができる。

a[n+1]=a[n]×r

等比数列の一般項

初項a, 公比r の等比数列

a, a×r , a×r2 ,………

第n項までに、公比r をn-1 個掛けることになるので、a[n]=a×r^(n-1)

初項a, 公比r の等比数列の一般項a[n]

a[n]=a×r^(n-1)

例11)では、a=2,r=3 → a[n]=2×3^(n-1)

(※a×r^(n-1) の形で処理することが多い。)

等比中項

a,b,cがこの順で等比数列のとき、

ac=b^2である。

大人の数学教室104(数列③)

【第3章】

(3)等差数列の和

例9)1から10までの自然数を足すといくらになるか。

S= 1+2+3+4+5+6+7+8+9+10 …①とおく。

足す順番を逆にすると、

S=10+9+8+7+6+5+4+3+2+ 1 …②

辺々を足す。

右辺は縦を足すと11が10 個できる。

(公差1, 公差-1 合わせると公差0)

2S=11×10 S=55

初項a, 公差d, 項数n の等差数列の和S[n]

末項l=a[n]=a+(n-1)d

S[n]=a+(a+d)+……+l→公差d

足す順番を逆にすると

S[n]=l……+(a+d)+a →公差-d

辺々を足す

右辺は縦を足すとa+l がn 個できる。

(公差d, 公差-d 合わせると公差0)

2S[n]=n(a+l)

S[n]=½×n(a+l)

初項a,末項l, 項数n の等差数列の和S[n]

S[n]=½×n(a+l)

l=a+(n-1)dだから、

初項a, 公差d, 項数n の等差数列の和S[n]

S[n]=½×n{2a+(n-1)d}

例10)1 からn までの自然数の和S[n]

初項1, 公差1, 項数n の等差数列の和だから

S[n]=½×n(n+1)

大人の数学教室103(数列②)

【第2章】

(2)等差数列

例6)1,3,5,7,9,11,13,15

隣り合った2 つの項に着目して、

差=(後ろの項)-(前の項) を考える。

2,2,2,2,2,2,2 → すべての差が等しい。

このように、隣り合った2 つの項の差がすべて等しい数列を「等差数列」といい、その差を「公差」という。

(後ろの項)=(前の項)+公差 だから、

初項と公差が決まれば、順々に項を作り、等差数列を作ることができる。

a[n+1]=a[n]+d

【等差数列の一般項】

初項a, 公差d の等差数列

a, a+d , a+2d ,………

第n項までに、公差d をn-1 個足すことになるので、a[n]=a+(n-1)d

初項a, 公差d の等差数列の一般項a[n]

a[n]=a+(n-1)d

例6)では、a=1,d=2

→ a[n]=1+(n-1)×2=2n-1

例7)k の倍数を小さい順に並べると、公差k の等差数列になる。

例8)k で割るとr 余る数を小さい順に並べると、公差k の等差数列になる。

等差中項

a,b,cがこの順で等差数列のとき、

a+c=2bである。

大人の数学教室102(数列①)

数列について考えよう。パズル感覚で考えると面白い分野です。

【第１章】

(1)数列

ある規則に従い数を1列に並べたものを 「数列」 という。

例1)1,3,5,7,9,11,13,15,17,19

規則→正の奇数を小さい順

例2)2,6,18,54,162

規則→最初が2, 順々に3 を掛ける

例3)1^2,2^2,3^2,4^2,5^2,……

規則→ n 番目が n^2

例4)1,2,4,7,11,16,……

規則→最初が1,順々に足す数が1ずつ増える

例5)1,1,2,3,5,8,13.……

規則→隣り合った2つの数を足して次を作る

それぞれの数を「項」という。

最初の項を「初項」、2番目の項を「第2項」、

n番目の項を「第n項」という。

項の個数を「項数」という。

項数が有限である数列を「有限数列」といい、最後の項を「末項」という。

項数が無限である数列を「無限数列」という。

例1),例2) は有限数列、例3)~例5)は無限数列

【数列の表記】

第n 項を a[n] と表す。(b[n],c[n],……)

数列 a[1],a[2],a[3],…,a[n],…

または

数列｛a[n]｝

(本来の表記は、aの右に小さくnと書く)

一般項

a[n]がnの式で表すことができるとき、

nに値を代入すれば任意の項が分かる。

このとき、a[n]を「一般項」という。

(注意) 一般項を表すとき、a[k]とも書ける。