自然科学ダイアログで、「時間と空間はどのように違うのか」を課題としてダイアログすることになり、この機会に自分の見解をまとめておこうと考えて検討に入った。この段階で、課題を念頭におきながら、量子力学の参考文献を読み直してみた。その結果、量子力学についての認識不足を痛感した。この課題を与えて下さった自然科学カフェの事務局に感謝したい。
特殊相対性理論では、光速不変の原理を基礎として、ニュートン力学の法則やマクスウェルの方程式などの自然法則は、互いに等速度運動をしている座標系に対しては同じ形になるべきであるとした。そのために、絶対時間という考えを捨て、ある事象の起こった場所と時刻を2つの座標系で各々観測するとき、両者の時刻が一般には等しくないとして、一方の座標系から観測する(位置、時刻)と他方の座標系から観測する(位置、時刻)との間の変換規則を定めた。この変換をローレンツ変換という。この変換式は、空間座標と時間とが同等に混じり合うこと(時間と空間の対称性)を示している。言い換えれば、自然法則は、ローレンツ変換に対して不変とみなすことができる。
量子力学の入門書では、シュレーディンガーの波動方程式がよく使われる。この方程式に基づき、パソコンを用いて固有関数と固有値を計算したことがある。また、水素原子のエネルギー準位と波動関数について学んだこともある。このような経験を経て、長い間、量子力学の基礎方程式とみなしてきたシュレーディンガーの波動方程式であるが、実はこの方程式は、ローレンツ変換に対する不変性を満たしていない。よって、「粒子の速さが光速度cに比べてずっと小さいときにしか適用できない」という制約がある。一方、ディラックによって提案された方程式は、エネルギー固有値がローレンツ変換に対して不変であることを前提として導かれたものであるから、ローレンツ変換に対する不変性という条件を満たしている。
以下、量子が電子であるとして、ディラックの方程式から導かれる波動関数と対応する固有値について述べる。ディラックのハミルトニアンは、4行4列の行列で表現されるので、これが作用する一粒子の波動関数は4つ存在することになり、4つ集まって電子の状態を指定している。ハミルトニアンの運動量に関する成分がすべて0とすると、電子が静止したときのエネルギー固有値を求めることができる。これらが電子の静止質量に対応するエネルギー量を表していて、2つの波動関数成分に対応する固有値が+mc^2、他の2つの関数成分に対応する固有値が-mc^2となる。
シユーレーディンガーのハミルトニアンは、電子の軌道角運動量に対応するエネルギー成分を含んでいるが、電子のスピン角運動量に対応するエネルギー成分を含んでいない。ディラックのハミルトニアンは、同軌道角運動量に対応する同成分とともに、同スピン角運動量に対応する同成分を含んでいる。スピン角運動量は、x,y,z方向のスピンの大きさを表す3つの4行4列の行列で構成される。各行列は、2行2列のパウリ行列を2組並べたものである。スピンに関する4つの波動関数のうち、2つの波動関数成分に対応する固有値が+バーh/2、他の2つの関数成分に対応する固有値が-バーh/2である。つまり、4成分の波動関数は、パウリの2成分の関数を2組並べたものになっている。この2組の一方が正エネルギーの状態、他方が負エネルギーの状態を表す。
シュレーディンガーの波動方程式では、電子は質量と負電荷だけをもつ質点として扱われているが、スピンをもつ量子として扱われていない。そのため、観測される原子スペクトルのエネルギー準位を説明するためにはスピン角運動量を導入する必要があった。こうしてみると、シュレーディンガーの波動方程式は、単に「粒子の速さが光速度cに比べてずっと小さいときにしか適用できない」とするだけでは不充分であり、より本質的な量子の扱いが必要になるのである。ディラックの方程式は、「任意の速度をもつ粒子に適用できる」ばかりではなく、負のエネルギー固有値をもつ粒子の存在を示唆するとともに、そのハミルトニアンHは電子スピンのエネルギーを含んでいるという重要な事実を内包しているのである。
ここで時空間の構造について考察する。時空が完全な真空である状態とは、それが負エネルギー状態の電子群で完全に埋められている状態と考える。そして正エネルギー状態の電子は、前者の電子群より高いエネルギー準位にあるため、安定に存在できる。しかし、電子群で詰まっている同じ真空上に正エネルギー状態の電子の居場所はあるのだろうか。電子は、その運動エネルギー量に応じた振動数をもつ波動であるから、正エネルギー電子は負エネルギー電子と同じ真空上に共存できるとみてよいのである。そこで、時空には電子がつくる量子場と呼ばれる内部構造が備わっていると考える。
ここまでのところ、量子場の自然法則は、ローレンツ変換に対して不変であり、時間と空間は原理的には同等のレベルにあり、両者の違いを見出せない。そこで、宇宙という巨大スケールの世界から量子力学が適用されるようなミクロなスケールの世界までを概観したときに、両者にはどのような違いがあるのかについて検討する。
まず、参考文献が言うように、「ものが動くから時間を認識できる」のである。たとえば、静止画だけだと空間の中には物体しかないから時間は不要であるが、パラパラ漫画や映画、テレビの画像のように空間中の物体が動くから時間を認識できる。こうしてみると、物体を収容する空間こそが主体的な存在であり、時間は従属的である。また、静止画には時間が介入しないが、動画像Aと次の動画像Bとは因果関係があり、必ず時間が介入するのである。
宇宙には、その誕生時から始まる空間と時間(宇宙年齢)がある。ここでも主体となるのは膨張する宇宙空間であり、時間は膨張した空間中に存在する天体から計測される従属的な存在である。よって空間は膨張するが時間が延びるとはみなされない。
一方、光速に近い速度で走る素粒子は、また異なった様相を見せる。たとえば、電子と同じく-1の電荷と1/2のスピンをもち、電子の約200倍の質量をもち、岩石の中を通過するほど透過性の高いミュー粒子を光速に近い速度で加速すると、静止したミュー粒子の崩壊寿命の約30倍の寿命をもつミュー粒子を観測できる。特殊相対性理論により、高速で運動するミュー粒子を静止座標系から見ると、時間が30倍に延びたように見えるのである。その一方で、空間に存在するミュー粒子の状態、つまり波動関数は静止系でも運動系でも不変とみなしているようである。ここでは、主役の空間の内容が不問であるから、脇役の時間を前面に出しているものとみる。
ダイアログは、東京大学の濱口幸一先生による30分ぐらいのガイダンスの後、先生を含めた参加者の自由な発言の場となった。私は、「時間は存在しない」とする説を信じる旨の発言をした。その理由として、「この説により、量子もつれに現れる非局所的長距離相関が当然のこととして説明できる」とした。私の発言に対して、事務局のスタッフかつダイアログ参加者から同意できないと受け取れる応答を返された。人間が時間軸を設定したとするには、設定した時間が理論と精緻に整合しているし、観測でも確認しているため、この説に違和感を覚えるということかも知れない。私は、この説を支持するが、空間は一般に非線形の式で表現されるのに対して、時間は常に線形にしか増減しないということで、両者の次元のランクに差があるのは、両者の主従関係を示唆しているのだろうか。
時間は常に線形にしか増減しないのは、マクロの世界の物理量を測定の対象とするからであろう。マクロの世界の測定値には無視できないほどの測定誤差が伴うのが常であるから、測定値は誤差を含めた範囲で理論値と一致するのであり、時間が線形増加でも充分通用するのであろう。ミクロの世界の理論値が時間について非線形であったとしても、測定誤差のためか不確定性原理のために測定不能となるのではなかろうか。
ダイアログは、先生のほかに20人の参加者が集まるという盛況ぶりとなった。ただ、数学的な議論が多く、ついて行けない場面が多かった。これといった結論はなかったが、インフレーションのある宇宙論についても先生とダイアログできて、有意義な会合であったと思う。
ダイアログの終了後に、単に「時間は存在しない」と主張するだけでは説明不充分であり、どのようにして現行の量子論と共存するのかについて説明しなければならないことに気がついた。
量子Aと量子Bは、量子もつれの相関関係はあるが、両者の間には相互関係が働かないか無視できるものとする。ここで量子Aと量子B各々の近傍には地平線を設定できるものと仮定する。そうすると、量子Aと量子Bは因果関係のない宇宙となるため、両量子間の関係性は、相対位置の変化だけであり、時間は無関係である。量子Aと量子B各々の宇宙の内部では相対論で言う固有時間が存在できるのだが、ここでは各量子は静止状態であって時間発展をしないため、時間は0で止まったまま量子の空間位置だけが変化することになる。このような状況では、時間並進対称性はないが、空間並進対称性があるので、量子の運動量が保存され、運動エネルギーが全エネルギーとなるので、エネルギーも保存される。こうなると、観測前の両量子の波動関数と相関関係は、両地平線を越えて保存されるので、量子Aの物理量を観測すれば、瞬時にして量子Bの対応する物理量が決まるのも当然の成り行きとなる。この相関関係が保存されるという仮定は、実験で確認されている。観測者が住む宇宙は、量子A,Bの宇宙とは別なので、量子AまたはBと接触することによって観測者は量子AまたはBの情報を得られるのだろうか。
参考文献
小出昭一郎著「量子力学I, II」(裳華房)
松浦壮著「時間とはなんだろう」(ブルーバックス)
広瀬立成著「超ひも理論と「影の世界」」(ブルーバックス)
特殊相対性理論では、光速不変の原理を基礎として、ニュートン力学の法則やマクスウェルの方程式などの自然法則は、互いに等速度運動をしている座標系に対しては同じ形になるべきであるとした。そのために、絶対時間という考えを捨て、ある事象の起こった場所と時刻を2つの座標系で各々観測するとき、両者の時刻が一般には等しくないとして、一方の座標系から観測する(位置、時刻)と他方の座標系から観測する(位置、時刻)との間の変換規則を定めた。この変換をローレンツ変換という。この変換式は、空間座標と時間とが同等に混じり合うこと(時間と空間の対称性)を示している。言い換えれば、自然法則は、ローレンツ変換に対して不変とみなすことができる。
量子力学の入門書では、シュレーディンガーの波動方程式がよく使われる。この方程式に基づき、パソコンを用いて固有関数と固有値を計算したことがある。また、水素原子のエネルギー準位と波動関数について学んだこともある。このような経験を経て、長い間、量子力学の基礎方程式とみなしてきたシュレーディンガーの波動方程式であるが、実はこの方程式は、ローレンツ変換に対する不変性を満たしていない。よって、「粒子の速さが光速度cに比べてずっと小さいときにしか適用できない」という制約がある。一方、ディラックによって提案された方程式は、エネルギー固有値がローレンツ変換に対して不変であることを前提として導かれたものであるから、ローレンツ変換に対する不変性という条件を満たしている。
以下、量子が電子であるとして、ディラックの方程式から導かれる波動関数と対応する固有値について述べる。ディラックのハミルトニアンは、4行4列の行列で表現されるので、これが作用する一粒子の波動関数は4つ存在することになり、4つ集まって電子の状態を指定している。ハミルトニアンの運動量に関する成分がすべて0とすると、電子が静止したときのエネルギー固有値を求めることができる。これらが電子の静止質量に対応するエネルギー量を表していて、2つの波動関数成分に対応する固有値が+mc^2、他の2つの関数成分に対応する固有値が-mc^2となる。
シユーレーディンガーのハミルトニアンは、電子の軌道角運動量に対応するエネルギー成分を含んでいるが、電子のスピン角運動量に対応するエネルギー成分を含んでいない。ディラックのハミルトニアンは、同軌道角運動量に対応する同成分とともに、同スピン角運動量に対応する同成分を含んでいる。スピン角運動量は、x,y,z方向のスピンの大きさを表す3つの4行4列の行列で構成される。各行列は、2行2列のパウリ行列を2組並べたものである。スピンに関する4つの波動関数のうち、2つの波動関数成分に対応する固有値が+バーh/2、他の2つの関数成分に対応する固有値が-バーh/2である。つまり、4成分の波動関数は、パウリの2成分の関数を2組並べたものになっている。この2組の一方が正エネルギーの状態、他方が負エネルギーの状態を表す。
シュレーディンガーの波動方程式では、電子は質量と負電荷だけをもつ質点として扱われているが、スピンをもつ量子として扱われていない。そのため、観測される原子スペクトルのエネルギー準位を説明するためにはスピン角運動量を導入する必要があった。こうしてみると、シュレーディンガーの波動方程式は、単に「粒子の速さが光速度cに比べてずっと小さいときにしか適用できない」とするだけでは不充分であり、より本質的な量子の扱いが必要になるのである。ディラックの方程式は、「任意の速度をもつ粒子に適用できる」ばかりではなく、負のエネルギー固有値をもつ粒子の存在を示唆するとともに、そのハミルトニアンHは電子スピンのエネルギーを含んでいるという重要な事実を内包しているのである。
ここで時空間の構造について考察する。時空が完全な真空である状態とは、それが負エネルギー状態の電子群で完全に埋められている状態と考える。そして正エネルギー状態の電子は、前者の電子群より高いエネルギー準位にあるため、安定に存在できる。しかし、電子群で詰まっている同じ真空上に正エネルギー状態の電子の居場所はあるのだろうか。電子は、その運動エネルギー量に応じた振動数をもつ波動であるから、正エネルギー電子は負エネルギー電子と同じ真空上に共存できるとみてよいのである。そこで、時空には電子がつくる量子場と呼ばれる内部構造が備わっていると考える。
ここまでのところ、量子場の自然法則は、ローレンツ変換に対して不変であり、時間と空間は原理的には同等のレベルにあり、両者の違いを見出せない。そこで、宇宙という巨大スケールの世界から量子力学が適用されるようなミクロなスケールの世界までを概観したときに、両者にはどのような違いがあるのかについて検討する。
まず、参考文献が言うように、「ものが動くから時間を認識できる」のである。たとえば、静止画だけだと空間の中には物体しかないから時間は不要であるが、パラパラ漫画や映画、テレビの画像のように空間中の物体が動くから時間を認識できる。こうしてみると、物体を収容する空間こそが主体的な存在であり、時間は従属的である。また、静止画には時間が介入しないが、動画像Aと次の動画像Bとは因果関係があり、必ず時間が介入するのである。
宇宙には、その誕生時から始まる空間と時間(宇宙年齢)がある。ここでも主体となるのは膨張する宇宙空間であり、時間は膨張した空間中に存在する天体から計測される従属的な存在である。よって空間は膨張するが時間が延びるとはみなされない。
一方、光速に近い速度で走る素粒子は、また異なった様相を見せる。たとえば、電子と同じく-1の電荷と1/2のスピンをもち、電子の約200倍の質量をもち、岩石の中を通過するほど透過性の高いミュー粒子を光速に近い速度で加速すると、静止したミュー粒子の崩壊寿命の約30倍の寿命をもつミュー粒子を観測できる。特殊相対性理論により、高速で運動するミュー粒子を静止座標系から見ると、時間が30倍に延びたように見えるのである。その一方で、空間に存在するミュー粒子の状態、つまり波動関数は静止系でも運動系でも不変とみなしているようである。ここでは、主役の空間の内容が不問であるから、脇役の時間を前面に出しているものとみる。
ダイアログは、東京大学の濱口幸一先生による30分ぐらいのガイダンスの後、先生を含めた参加者の自由な発言の場となった。私は、「時間は存在しない」とする説を信じる旨の発言をした。その理由として、「この説により、量子もつれに現れる非局所的長距離相関が当然のこととして説明できる」とした。私の発言に対して、事務局のスタッフかつダイアログ参加者から同意できないと受け取れる応答を返された。人間が時間軸を設定したとするには、設定した時間が理論と精緻に整合しているし、観測でも確認しているため、この説に違和感を覚えるということかも知れない。私は、この説を支持するが、空間は一般に非線形の式で表現されるのに対して、時間は常に線形にしか増減しないということで、両者の次元のランクに差があるのは、両者の主従関係を示唆しているのだろうか。
時間は常に線形にしか増減しないのは、マクロの世界の物理量を測定の対象とするからであろう。マクロの世界の測定値には無視できないほどの測定誤差が伴うのが常であるから、測定値は誤差を含めた範囲で理論値と一致するのであり、時間が線形増加でも充分通用するのであろう。ミクロの世界の理論値が時間について非線形であったとしても、測定誤差のためか不確定性原理のために測定不能となるのではなかろうか。
ダイアログは、先生のほかに20人の参加者が集まるという盛況ぶりとなった。ただ、数学的な議論が多く、ついて行けない場面が多かった。これといった結論はなかったが、インフレーションのある宇宙論についても先生とダイアログできて、有意義な会合であったと思う。
ダイアログの終了後に、単に「時間は存在しない」と主張するだけでは説明不充分であり、どのようにして現行の量子論と共存するのかについて説明しなければならないことに気がついた。
量子Aと量子Bは、量子もつれの相関関係はあるが、両者の間には相互関係が働かないか無視できるものとする。ここで量子Aと量子B各々の近傍には地平線を設定できるものと仮定する。そうすると、量子Aと量子Bは因果関係のない宇宙となるため、両量子間の関係性は、相対位置の変化だけであり、時間は無関係である。量子Aと量子B各々の宇宙の内部では相対論で言う固有時間が存在できるのだが、ここでは各量子は静止状態であって時間発展をしないため、時間は0で止まったまま量子の空間位置だけが変化することになる。このような状況では、時間並進対称性はないが、空間並進対称性があるので、量子の運動量が保存され、運動エネルギーが全エネルギーとなるので、エネルギーも保存される。こうなると、観測前の両量子の波動関数と相関関係は、両地平線を越えて保存されるので、量子Aの物理量を観測すれば、瞬時にして量子Bの対応する物理量が決まるのも当然の成り行きとなる。この相関関係が保存されるという仮定は、実験で確認されている。観測者が住む宇宙は、量子A,Bの宇宙とは別なので、量子AまたはBと接触することによって観測者は量子AまたはBの情報を得られるのだろうか。
参考文献
小出昭一郎著「量子力学I, II」(裳華房)
松浦壮著「時間とはなんだろう」(ブルーバックス)
広瀬立成著「超ひも理論と「影の世界」」(ブルーバックス)










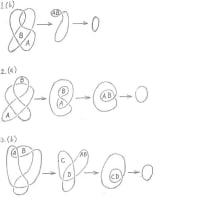


※コメント投稿者のブログIDはブログ作成者のみに通知されます