平成29年度大阪府教員チャレンジテストからです。 次の表は、ある高校の3年生が大学P及び大学Qで実施された入学者選抜試験を受験した結果を示したものである。入学者選抜試験には前期日程と後期日程の二種類があり、前期日程の合格発表の後に後期日程の試験が実施される。出願の締切日は前期日程、後期日程の両方とも前期日程の試験が始まる約1か月前に設定されている。出願できる大学は、受験生一人につき前期日程、後期日程でそれぞれ一つまでとなっており、前期日程と後期日程で異なる大学に出願することもできる。
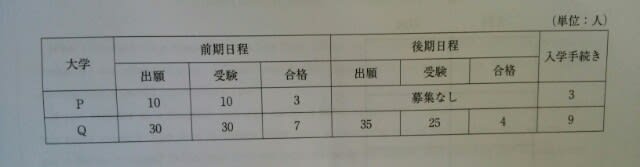
大学P及び大学Qの入学者選抜試験の結果について、次のア及びイのことが分かっている。ア 後期日程で大学Qに出願した人は、必ず前期日程で大学Pまたは大学Qに出願している。イ 前期日程で合格した人は、後期日程は受験していない。このとき、確実にいえるものはどれか。1～5から一つ選べ。
肢1……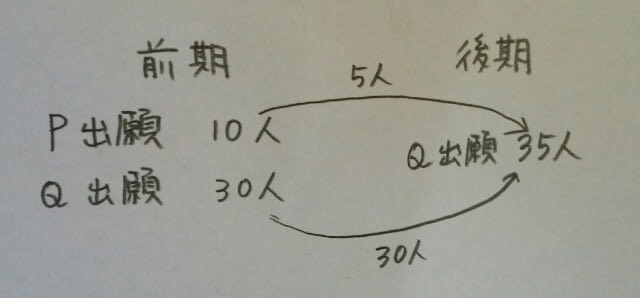
なので、これが正解と考えるのは、ちょっと……😢前期日程でQに出願した人が必ず後期日程にも出願したとは限りませんね。
など、反例は5通り考えられます。 肢2……前期日程で不合格となった人は、Pで7人、Qで23人の計30人。後期日程を受験した人は25人だから、確かに5人は後期日程を受験していないので、一見これが正解のような気がしますが、「後期日程で大学Qに出願したにもかかわらず」という文言が気になります。 後期日程で大学Qに出願したにもかかわらず受験しなかったひとは、35－25＝10人います。何でそんなもったいないことをするのでしょう？ 受験料といったって、1万円以上はするでしょう。そんなお金があったら、ギョウザを何人前食べれるでしょう？ああ、もったいない、親は泣いています。少し脱線しましたが、その10人は、前期日程で合格したから、もう後期日程は受験する必要がなかったからだと考えるのが一番自然ですね。表を見ても、ちょうど10人が前期日程で合格しています。つまり、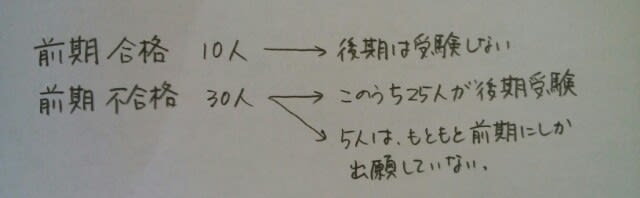
という反例ができます。一番自然な状態を考えるというのは、前にも出題されていて、興味のある方は、カテゴリー「その他」17年9月9日の記事を覗いてみて下さい。 肢3……条件アより、後期日程でQを受験（出願）した人は、必ず前期日程でPまたはQを受験（出願）しています。（前期日程を欠席した人はいません）。 もしも、後期のQを受験した人の中に、前期のPを受験した人がいないとしたら…。 前期のQで不合格だった人は23人なので、後期を受験した人が25人もいるはずがありませんね。「いやいや、前期で合格した人が、後期も受験したかもしれない」と思った人は、条件イを読んで下さい。よって、肢3が正解です。 肢4……後期日程でQに合格したのは4人ですが、この4人は全員前期日程でもQ大学を受験して不合格だった人かもしれません。（Q大学の前期日程で不合格の人23人が全員後期日程にも出願していて、そのうちの4人が合格したということがあり得ます。） 肢5……前期日程を受験した人は40人で、前期後期合わせて14人が合格し、両方合格した人はいない（条件イ）ので、いずれにも合格できなかった人は26人です。ここをポチッとお願いします。→
にほんブログ村
