単なる加減乗除の計算ですが、よく出題されます。 例えば、2019年度の神奈川県。正誤判定ですが、
実際は、これを計算すると20であるというのが正しいか誤りかを判定する問題です。 我々、小学生のとき、かっこがあれば、かっこの中を先に計算し、掛け算や割り算は、足し算や引き算よりも先に計算するべしと習ったわけですが、中学になると、指数が登場するので、結局、①指数②かっこ③乗除④加減の順に計算するということになりましたね。よって、こうなります。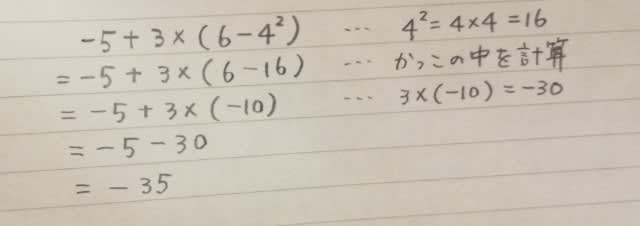
ところで、計算問題をたくさん解いていると、0.25や0.75という小数がしょっちゅう出てきますね。 はじめのうちは、0.25は100分の25で、これを約分していくと4分の1になって、などとやるのですが、いつか、0.25は4分の1、0.75は4分の3だと覚えてしまいます。 もっと慣れてくると、0.125が8分の1、0.375が8分の3、0.625が8分の5、0.875が8分の7も覚えてしまい、3.5なども、7の半分だから、2分の7とできるようになります。 同じく2019年度愛媛県では、こうです。
やってみます。
け、計算ドリルやるべき?ここをポチッとお願いします。→
にほんブログ村


実際は、これを計算すると20であるというのが正しいか誤りかを判定する問題です。 我々、小学生のとき、かっこがあれば、かっこの中を先に計算し、掛け算や割り算は、足し算や引き算よりも先に計算するべしと習ったわけですが、中学になると、指数が登場するので、結局、①指数②かっこ③乗除④加減の順に計算するということになりましたね。よって、こうなります。
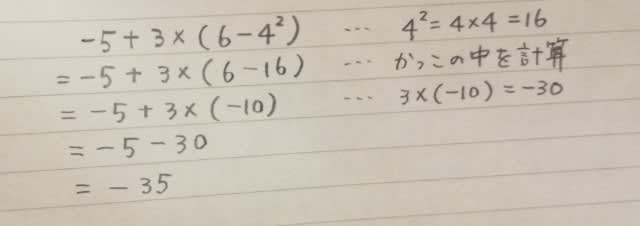
ところで、計算問題をたくさん解いていると、0.25や0.75という小数がしょっちゅう出てきますね。 はじめのうちは、0.25は100分の25で、これを約分していくと4分の1になって、などとやるのですが、いつか、0.25は4分の1、0.75は4分の3だと覚えてしまいます。 もっと慣れてくると、0.125が8分の1、0.375が8分の3、0.625が8分の5、0.875が8分の7も覚えてしまい、3.5なども、7の半分だから、2分の7とできるようになります。 同じく2019年度愛媛県では、こうです。

やってみます。

け、計算ドリルやるべき?ここをポチッとお願いします。→
にほんブログ村











