最もシンプルなのは問題の通りに書き出してみることでしょうか。
容器Aと容器Bの容積の差は120立方センチメートルという条件が与えられていますが、Aだと7はい目の途中、Bだと12はい目の途中でいっぱいになるのですから、Aの方が容積が大きいと分かりますね。
ですから、A1はいを、(B1はい+120立方センチメートル)と考えます。〔条件1〕
水そうの容積について、問題文から、次の二通りに表せます。
まず一つ目の表し方。
容器Aの7はい目に100立方センチメートル残ることから
A7はい-100立方センチメートル
となります。
これは〔条件1〕により、次のように置き換えられます。
A7はい=B7はい+120立方センチメートル×7なので
(B7はい+120立方センチメートル×7)-100立方センチメートル
整理しましょう。
B7はい+840立方センチメートル-100立方センチメートル
B7はい+740立方センチメートル〔条件2〕
次に二つ目の表し方。
容器Bの12はい目に160立方センチメートル残ることから
B12はい-160立方センチメートル〔条件3〕
〔条件2〕と〔条件3〕はどちらも水そうの容積を表していますから等しいです。
つまり
B7はい+740立方センチメートル=B12はい-160立方センチメートル
線分図に表してみましょう。
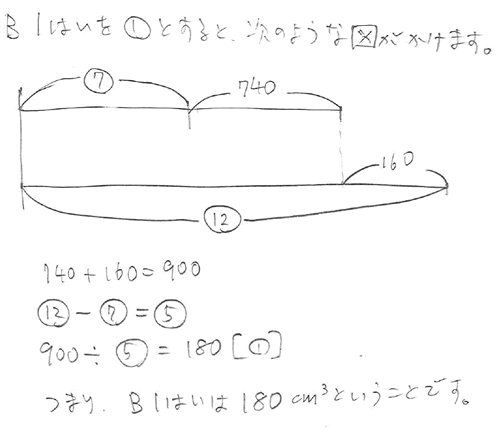
180立方センチメートル×12-160立方センチメートル=2000立方センチメートル
答え2000立方センチメートル
このほか、面積図によって解くのも良いやり方だと思います。
容器Aと容器Bの容積の差は120立方センチメートルという条件が与えられていますが、Aだと7はい目の途中、Bだと12はい目の途中でいっぱいになるのですから、Aの方が容積が大きいと分かりますね。
ですから、A1はいを、(B1はい+120立方センチメートル)と考えます。〔条件1〕
水そうの容積について、問題文から、次の二通りに表せます。
まず一つ目の表し方。
容器Aの7はい目に100立方センチメートル残ることから
A7はい-100立方センチメートル
となります。
これは〔条件1〕により、次のように置き換えられます。
A7はい=B7はい+120立方センチメートル×7なので
(B7はい+120立方センチメートル×7)-100立方センチメートル
整理しましょう。
B7はい+840立方センチメートル-100立方センチメートル
B7はい+740立方センチメートル〔条件2〕
次に二つ目の表し方。
容器Bの12はい目に160立方センチメートル残ることから
B12はい-160立方センチメートル〔条件3〕
〔条件2〕と〔条件3〕はどちらも水そうの容積を表していますから等しいです。
つまり
B7はい+740立方センチメートル=B12はい-160立方センチメートル
線分図に表してみましょう。

180立方センチメートル×12-160立方センチメートル=2000立方センチメートル
答え2000立方センチメートル
このほか、面積図によって解くのも良いやり方だと思います。

















