スプライン曲線で花びらを描く

　１月２７日付のブログで紹介したスプライン曲線の続きとして、最小限のデータ点を与えてスプライン補間し、花びらのような閉曲線を描けるのか否か試してみることにした。

　花びらのデータ（ｘj，ｙj）；（ｊ＝１，２，．．．，Ｎ）は、平面データであるから、一価関数の形をしていない。そこで、データ点の位置を極座標で表現することにし、データ点の位置を示す動径ｒは偏角ｔの関数とみる。ｔは０から２パイまでの区間に存在すればよい。

　花びらは５弁とし、花びら図形の山の頂点で５点、谷の頂点で５点、合計１０点のデータ点をとり、これらデータ点の間をスプライン補間するものとする。山の頂点でｒ＝６、谷の頂点でｒ＝２としてみた。

　花びら山を中点とする区間と花びら谷を中点とする区間の大きさを均等にとるのではなく、パイ／１５を１単位として前者では４単位、後者では２単位の区間とした。これによってＢスプライン関数は、２単位区間用の関数と４単位区間用の関数の２種類できることになる。

　区間［０，２パイ］の０境界と２パイ境界では、節点が多重化するので、境界近くでは１個の２次式片のＢスプラインと２個の２次式片を連結したＢスプラインとが現れる。このため、３個の２次式片を連結した上記のＢスプライン関数の配列の規則性が失われる。区間［０，２パイ］でこの規則性を保持するために、境界附近のＢスプラインを設けるために、両端に余分な５単位の領域を追加し、区間を［０－５単位，２パイ＋５単位］とした。

　３連結のＢスプライン関数は、その中点に関して対称関数である。また、花びら山と花びら谷のスプライン曲線も各々その中点に関して対称であればよい。従って、Ｂスプライン関数の両端の２次式片のＢスプライン係数は等しくなる。そうすると、Ｂスプライン係数を求めるための連立方程式は、２単位区間用のＢスプラインの線形結合式と４単位区間用のＢスプラインの線形結合式の２式だけとなり、未知の係数は２個となり、係数の算出は容易である。

　Ｂスプライン曲線を１単位について１０個の点列で表現することにすると、計算に関与する区間は［－５０，３５０］であり、Ｅｘｃｅｌでは１つずつ加算する整数の連続データを生成すればよい。そうすると、偏角ｔは、各整数＊ＰＩ（）／１５０で表せる。

　動径ｒはｔの関数となり、３個のＢスプラインの線形結合式で表現する。各区間の最初の整数に対応してｒの計算式を設定し、この計算式をその区間の最後のｒまでコピーする。

　このようにして、各区間についてｒの値が計算できたら、その中点のｔについて意図したデータ値（ｒ＝６または２）になっていることを確認する。

　すべてのｒの計算ができたら、区間［０，３００］に対応するｒについて、ｘ＝ｒｃｏｓｔ，ｙ＝ｒｓｉｎｔの計算式により、（ｘ，ｙ）の値を計算する。

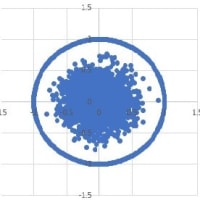
　図は、（ｘ，ｙ）の値を散布図としてグラフ表示したものである。



　このグラフを見ると、スプライン補間の技法を利用し、２次式のスプライン曲線によって１０点のデータから５弁の花びら図形を描けることが分かる。

　Ｅｘｃｅｌのグラフ表示では、ｘ軸の目盛間隔とｙ軸の目盛間隔が等しくなるとは限らない。このため、花びらの図形は、やや歪んだものとなった。

　参考文献
　吉本富士市著「インターネット時代の数学―スプライン」（共立出版）