前回(60)の続きで、「すぐに役立つ統計のコツ」(オーム社)をもとに書いています。
本書の立ち読みは下記URLからど~ぞ!
本書の立ち読みは下記URLからど~ぞ!
http://www.e-hon.ne.jp/bec/SA/Detail?refShinCode=0100000000000033365048&Action_id=121&Sza_id=B0
それでは、今回はSPSSで正準判別分析をやって見ましょう。その前に、
杉本典夫先生(統計学入門)からのコメントの一部をご紹介しておきます。
***
ロジスティック回帰分析は前向き研究から得られたデータに適用する手法です。
・・・
ロジスティック回帰分析は、最初から前向き研究用の手法として開発されたのです。
そのため後ろ向き研究から得られたデータには判別分析を適用し、
必要に応じて有病率(事前確率)とロジスティック曲線を利用して、
判別スコアを予測確率に変換するのが本来の使い方です。
***
ロジスティック回帰分析は前向き研究から得られたデータに適用する手法です。
・・・
ロジスティック回帰分析は、最初から前向き研究用の手法として開発されたのです。
そのため後ろ向き研究から得られたデータには判別分析を適用し、
必要に応じて有病率(事前確率)とロジスティック曲線を利用して、
判別スコアを予測確率に変換するのが本来の使い方です。
***
SPSSを立ち上げて下さい。
Excelで作成しているなら、コピー&ペーストで SPSS の"データエリア"に取込むことが出来ます。
Excelで作成しているなら、コピー&ペーストで SPSS の"データエリア"に取込むことが出来ます。
そして、
分析→分類→判別分析→グループ変数[fDiag]→範囲の定義をクリック→最小[0],最大[1]→続行→独立変数[SBMG, UBMG, UBMG]→統計→関数係数[☑標準化されていない]→続行→分類→
[◎すべてのグループが等しい、◎グループ内、☑ケースごとの結果、☑集計表]→続行→OK
分析→分類→判別分析→グループ変数[fDiag]→範囲の定義をクリック→最小[0],最大[1]→続行→独立変数[SBMG, UBMG, UBMG]→統計→関数係数[☑標準化されていない]→続行→分類→
[◎すべてのグループが等しい、◎グループ内、☑ケースごとの結果、☑集計表]→続行→OK
色々な統計量が出力されますが、ここでは最小限の表示を紹介します。
SPSSの出力結果:

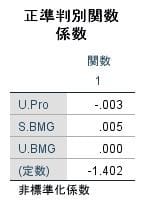
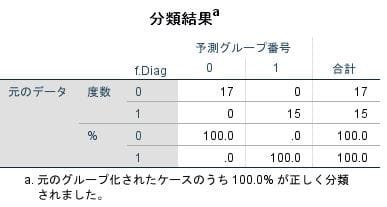
以上の様に、SPSSでは "正準判別分析" の結果が返されます。
「R」での"正準判別分析"のライブラリーには次の「candisc」があります。
やって見ましょう。
***
# 前回と同じ要領でデータを取り込む。
# 前回と同じ要領でデータを取り込む。
dat<- read.delim("clipboard", header=T)
head(dat)
s.dat<- scale(dat[, 2:4]) # データの標準化
dat1<- cbind(dat, s.dat) # 原データと標準化データの結合
head(dat1)
head(dat)
s.dat<- scale(dat[, 2:4]) # データの標準化
dat1<- cbind(dat, s.dat) # 原データと標準化データの結合
head(dat1)
y1<- dat1[, 1]
x1<- dat1[, 2]
x2<- dat1[, 3]
x3<- dat1[, 4]
x1<- dat1[, 2]
x2<- dat1[, 3]
x3<- dat1[, 4]
fit.lm <- lm( cbind(x1,x2, x3)~ y1) # 説明変数(x)と目的変数(y)の配置に注意。
library(candisc) # 事前にインストールしておく
fit.disc <- candisc(fit.lm)
fit.disc
summary(fit.disc, means=T, scores=F, coef=c("raw"))
fit.disc
summary(fit.disc, means=T, scores=F, coef=c("raw"))
主な出力結果:
raw coefficients: # 各説明変数の係数
x1 x2 x3
-0.00305863 -0.01468579 0.00011609
x1 x2 x3
-0.00305863 -0.01468579 0.00011609
(x1=U.Pro、x2=S.BMG、x3=U.BMG)
***
***
ここでの出力結果(係数)は、SPSSと異なっていますが判別結果は同じです。この係数は前回のパッケージ・ライブラリー(lda)の結果と一致しており、関数(lda)は、説明変数が3つ以上のとき正準判別分析の結果が返されるようです。
なお、
標準化された正準判別関数の係数は、標準化データ(dat1)について実行すれば良いでしょう。
標準化された正準判別関数の係数は、標準化データ(dat1)について実行すれば良いでしょう。
参考までに、
"SAS-JMP"の判別分析もご紹介しておきます。
"SAS-JMP"の判別分析もご紹介しておきます。
分析の手順;
JMPを立上げ→分析→多変量→判別分析→Y.共変量[U.Pro, S.BMG, U.BMG]→X.カテゴリ[fDiag]→OK
→結果の出力→判別分析→正準オプション→正準詳細を表示→▶スコアリング係数→図1・表1
JMPを立上げ→分析→多変量→判別分析→Y.共変量[U.Pro, S.BMG, U.BMG]→X.カテゴリ[fDiag]→OK
→結果の出力→判別分析→正準オプション→正準詳細を表示→▶スコアリング係数→図1・表1
図1 正準散布図

表1 正準判別係数

"SAS-JMP"の判別係数は「R」と一致していました。
情報統計研究所はここから!


















