「すぐに役立つ統計のコツ」(オーム社)には載せてませんが、
前回の主成分分析と関連して、「R」による因子分析の概要をご紹介します。
***
dat<- read.delim("clipboard", header=T)
head(dat)
dat<- read.delim("clipboard", header=T)
head(dat)
fa1<- factanal(dat, factors = 3, rotation = "promax", scores = "regression", method = "pa") # 斜交回転:promax
fa1
fa1
出力結果:
Call:
factanal(x = dat, factors = 3, scores = "regression", rotation = "promax", method = "pa")
Call:
factanal(x = dat, factors = 3, scores = "regression", rotation = "promax", method = "pa")
Uniquenesses:
WBC IgE Eo Ba St Cmin
0.647 0.670 0.005 0.688 0.478 0.488
WBC IgE Eo Ba St Cmin
0.647 0.670 0.005 0.688 0.478 0.488
Loadings:
Factor1 Factor2 Factor3
WBC -0.336 0.254 0.340
IgE 0.583
Eo 0.178 1.021
Ba -0.428 0.178 -0.292
St 0.723
Cmin 0.734 0.191
Factor1 Factor2 Factor3
WBC -0.336 0.254 0.340
IgE 0.583
Eo 0.178 1.021
Ba -0.428 0.178 -0.292
St 0.723
Cmin 0.734 0.191
Factor1 Factor2 Factor3
SS loadings 1.207 1.184 0.727
Proportion Var 0.201 0.197 0.121
Cumulative Var 0.201 0.399 0.520
SS loadings 1.207 1.184 0.727
Proportion Var 0.201 0.197 0.121
Cumulative Var 0.201 0.399 0.520
Factor Correlations:
Factor1 Factor2 Factor3
Factor1 1.0000 0.220 0.0318
Factor2 0.2200 1.000 0.0730
Factor3 0.0318 0.073 1.0000
Factor1 Factor2 Factor3
Factor1 1.0000 0.220 0.0318
Factor2 0.2200 1.000 0.0730
Factor3 0.0318 0.073 1.0000
The degrees of freedom for the model is 0 and the fit was 0
***
***
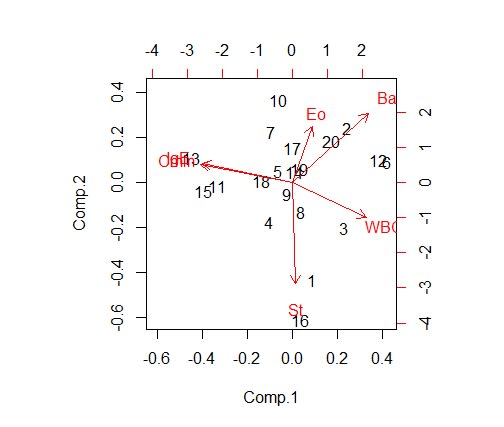
図1:主成分負荷量と主成分得点

図1を見ると、WBCとBaの矢印が同じ方向に向いており角度も小さいことが分かります。同じように、CminとIgEも同方向で角度が小さいです。
このことから、
気管支喘息患者での"WBCとBa"、"IgEとCmin"は関連性のある因子と思われます。すなわち、"白血球数と好塩基球数"、"気道過敏性とIgE"です。
このことから、
気管支喘息患者での"WBCとBa"、"IgEとCmin"は関連性のある因子と思われます。すなわち、"白血球数と好塩基球数"、"気道過敏性とIgE"です。
これは、大体、臨床的に納得できるでしょうか・・・?
統計のコツは、まず実行して見ることです。
「すぐに役立つ統計のコツ」(オーム社)は、統計分析の実践を通じて統計的な方法を学ぶことが出来ると思います。
そうです~、学ぶより慣れることが統計分析のコツかも知れませんね!
そして、
疑問な点が一杯でて来るでしょう・・から、その疑問を専門書やインターネットなどで調べて行けば自然に統計的方法が身につくことでしょう。
「すぐに役立つ統計のコツ」(オーム社)は、統計分析の実践を通じて統計的な方法を学ぶことが出来ると思います。
そうです~、学ぶより慣れることが統計分析のコツかも知れませんね!
そして、
疑問な点が一杯でて来るでしょう・・から、その疑問を専門書やインターネットなどで調べて行けば自然に統計的方法が身につくことでしょう。
「すぐに役立つ統計のコツ」(オーム社)に掲載されているエクセルの「例題」(データ)は、情報統計研究所のホームページからダウンロード出来ますので
ご利用下さい。
ご利用下さい。
次回は、
「すぐに役立つ統計のコツ」の最終章(第8章)をご紹介します。
「すぐに役立つ統計のコツ」の最終章(第8章)をご紹介します。

情報統計研究所はここから!