ビジネスと統計（5）

前稿までの野菜価格は各月の上旬・中旬・下旬におけるものですので、これを時系列データと言います。この様な時系列データは気候や物価変動などの影響を受けるものです。今回は、
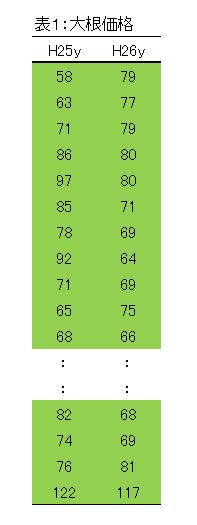
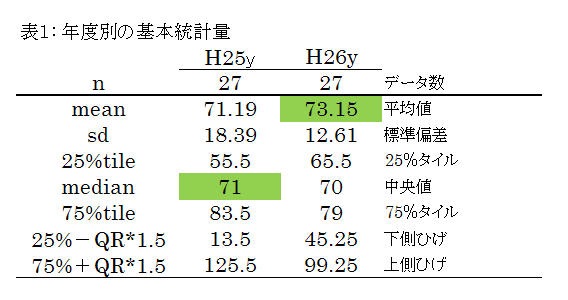
大根・白菜・ピーマン・馬鈴薯の価格を表1 に示しました。この３つの野菜の相関関係は表2 の様な相関行列で示す事が出来ます。




MS-Excel (2010 ver) では次の様にすれば良いでしょう。
　・データ→データ分析
　　「データ分析] コマンドが表示されない場合は、分析ツールアドインプログラムを読み込む。
　・相関→入力範囲（表1の緑色部分）→☑先頭行をラベルとして使用→出力先（任意に空白セルを指定）
　・OKをクリック
　・表2の相関行列が得られる。

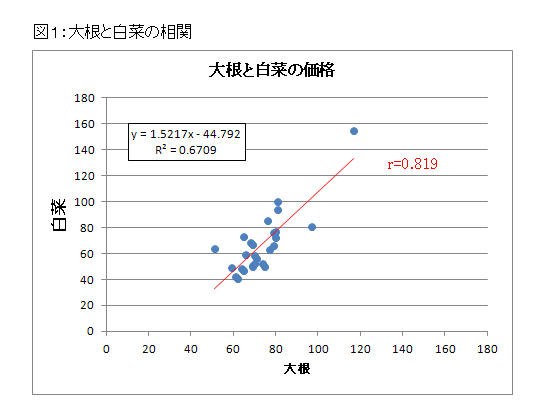
表2の「大根と白菜」の相関係数はｒ＝0.819、「ピーマンと馬鈴薯」の相関係数はｒ＝-0.676　であり、相関関係が強いと言えます。ここで、「大根と白菜」は正(+)の相関が、「ピーマンと馬鈴薯」は負(-)の相関(逆相関とも言う)があると言えます。

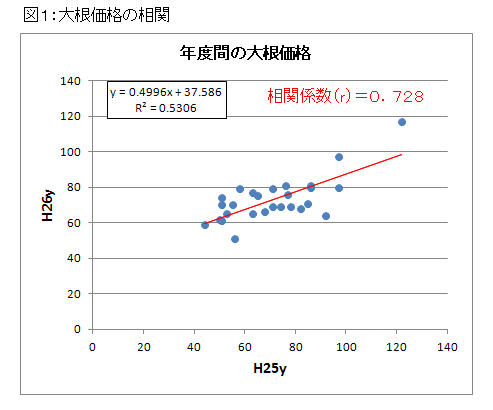
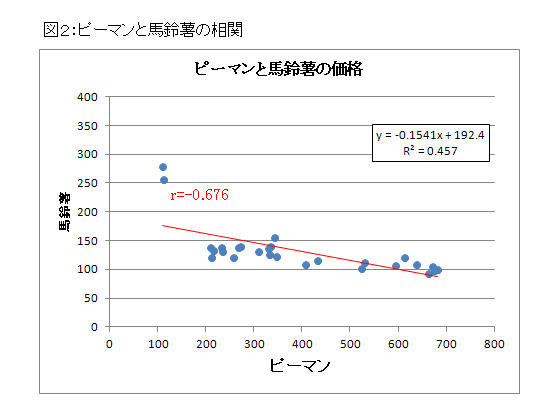
この関係を、図1・図2 の相関散布図(回帰直線)にすると分かり易いでしょう。
図1では、大根が高いときは白菜も高いことが分かります。
図2では、ピーマンが高くなれば馬鈴薯は安くなる様です(ピーマンの旬は６月・７月・８月、馬鈴薯の旬は10月・11月)。




もちろん、
季節性や物価動向などに左右されますので、それらの影響を見極める必要があります。その様な影響因子に関する分析はまたの機会とします。ここでは、
ビジネスでの色々な場面での統計的方法(相関)を体験してみて下さい。

次回に続く！

情報統計研究所はここから。

ビジネスと統計（４）

ここでは野菜価格を例題としていますが、ビジネスにおけるデータでも、同様の手法で要約し視覚化すると内在する情報の特徴が分かり易くなります。
それでは、
大根価格を25年度（H25y）と26年度（H26y）で比べてみましょう。今回は両年度における相関関係を見てみます。

表1はH25yとH26y における大根価格であり、図1はその相関散布図で横軸にH25yを縦軸にH26yの大根価格をとって描いています。




MS-Excel (2010 ver) での作成は次の様にすれば良いでしょう。
　・表１の緑色セル部分を選択
　・挿入→散布図→散布図（マーカのみ）を選択
　・散布図の１つのプロットを右クリック
　・近似曲線の追加→線形近似→□ グラフに数式を表示する→□ グラフにR-2乗値を表示する→□にチェック→閉じる
　　
図1を参考に見やすく編集して下さい。

図1の赤色直線を回帰直線と言いH25yとH26yの大根価格は同じ様に変動していることを表しています。
ビジネスにおいても２つのデータがあれば、例えば「投資と売上」とか「販売価格と数量」とか・・・色々で試して下さい。
ここでは、
赤字で示した相関係数(r＝0.728)に注目です。この値は相関の強さを表しており「1」に近いほど相関が強いと言えます。
図1の赤色直線の傾き具合によって、H25yとH26yの大根価格に差が有るかどうかを、また散布点(プロット)のバラツキ具合で相関の具合などを推測出来ます。
ただ、
「相関が無い＝関連性（規則性）がない」では有りません。「相関がある」とは図1の赤色直線にそって多くのデータが散布することだと言えます。

相関と回帰はビジネス統計で大切な手法かと思いますので、追々、説明して行きたいと思います。

次回に続く！

情報統計研究所はここから

ビジネスと統計（３）

大根価格を25年度と26年度で比較して見ましょう。やはり、中四国農政局のHPから引用します。
両年度年度の大根価格の統計量とBoxPlot は表１と図1(前稿参照)の様になりました。


表1では、平均値と中央値の大きさが異なっています。この様に、平均値を大根価格の代表値とすれば26年度の方が高くなり、中央値を代表値とすれば僅かに安くなります。ビジネスにおいても平均値が必ずしも代表値として正しいかどうかは分かりません。平均値は飛び離れた値の影響を受けますので、その様なときは中央値や最頻値などを用いるなど代表値の長所・短所を知って用いるべきでしょう。

表1 の統計量は図1 のBoxPlot で表すことが出来ます。


図1 の「Wilcoxon の検定結果」に付いては別稿で述べますので、ここではBoxPlot での表現法を感じ取って下さい。
BoxPlot（図1）を見ると、25年度の上ひげ（上側の縦線）が長いです。すなわち、高値の方にバラツキが見られる事が分かります。
それに比べて、２６年度の上下ひげ（上下の縦線）は同じくらいであり、バラツキが少ないと言えます。
この様にグラフにすると、その違いが分かり易くなりますので、ビジネスにおいても積極的に BoxPlotで統計量を要約しプレセンすれば一目置かれるかも知れませんよ・・・！

データのバラツキ具合は「平均値±標準偏差」で表すのでは・・・？　
それでは計算して見ましょう。
　25年度の場合：平均値±標準偏差＝52.8 ～89.58
26年度の場合：平均値±標準偏差＝60.54～85.76

平均値を挟んでバラツキが均等な正規分布の時は「平均値±標準偏差」をお勧めします。

たぶん、ビジネスで経験する多くのデータは正規分布でないと思われますので、ここでの例題（野菜価格）では積極的に BoxPlot の方法をご紹介したいと思います。
ちなみに、
BoxPlot は統計学的にノンパラメトリック法に適用されますが、専門用語は今のところパスしておきましょう。

次回に続く！

情報統計研究所はここから

ビジネスと統計（2）

全稿では、野菜価格（大根）の統計量要約でBoxPlot を示しました。大根の価格は平均値の上下で価格のバラツキが見られます(前稿：図１)。すなわち、
この様なバラツキのあるデータは正規分布と言えません。正規分布とは平均値を挟んでその上下でのバラツキが同じ様なデータを言います。正規分布であるかないかは、統計分析上とても大切な基本情報ですので、詳しくは下記URLを参照し覚えておいて欲しいと思います。
　やさしい医学統計手法

ビジネス現場でのほとんどのデータは正規分布と言えない場合が多いので、最近では（大標本の場合はとくに）BoxPlot で表現する事が多くなっています。それでは、
BoxPlot の作成の実際を MS-Excel（Excel 2010） で紹介します。
大根価格の場合：
　１．表1（緑色部分）を作成
　２．緑色部分を選択
　３．「挿入」→「その他のグラフ」→「株価チャート（始値・高値・安値・終値）」


Excel での BoxPlot 作成では表1の様に日付を1月1日などと適当に付け、「75%tile、75%tile+QR*1.5、25%tile-QR*1.5、25%tile」を当てはめ株価チャートを作成した後に、日付（1月1日）を大根に変更し、凡例を削除し、中央値を Boxの中に描画すれば BoxPlot になります。ただ、
BoxPlot の上下の縦線（ひげ）は適当に設定しても良いのですが、通常は、上ひげでは「75%tile+QR*1.5」に最も近い値（ここでは97を）、下ひげでは「25%tile-QR*1.5」の最も近い値（ここでは51）を用います。
最大値・最小値や標準偏差値にしたときは必ず明記しておきましょう。詳しくは、
情報統計研究所の「やさしい医学統計手法」を見て下さい。

さあ・・！
BoxPlot を積極的に使ってビジネスデータを要約して見ましょう。

次回に続く！

情報統計研究所はここから