前回はデータ記述の散布図表現について紹介しました。今回は数値要約の例を紹介したいと思います。データの代表値は「平均値±1標準偏差」(正規分布のときなど)、あるいは、中央値[25%タイル、75%タイル](非正規分布のときなど)を用いて表現します。前回、探索的データ分析では Box Plot で示すことが多くなったと言いましたが、数値記述でも5数要約である「最小値、下側ヒンジ、中央値、上側ヒンジ、最大値」で示すことが多く見受けられるようです。 これは1つに統計ソフト(パッケージ)の普及によって、数値要約や図表要約が簡単に出来るようになったことと、もう1つは、正規母集団分布での推測統計から、母集団分布に拘わらないノンパラメトリックの積極的な使用が多くなったことが挙げられます。5数要約での下側ヒンジは第1四分位数、上側ヒンジは第3四分位数であり、下・上クオンタイル(quantile)と呼ばれ、そして、クオンタイルの確率がパーセント点(parcentile)です。
これは1つに統計ソフト(パッケージ)の普及によって、数値要約や図表要約が簡単に出来るようになったことと、もう1つは、正規母集団分布での推測統計から、母集団分布に拘わらないノンパラメトリックの積極的な使用が多くなったことが挙げられます。5数要約での下側ヒンジは第1四分位数、上側ヒンジは第3四分位数であり、下・上クオンタイル(quantile)と呼ばれ、そして、クオンタイルの確率がパーセント点(parcentile)です。
今回はデータや統計的記述の視覚的な表現である散布図(Scatter Plot)について紹介します。散布図としては2変量の関係を見る2組の相関散布図や3組以上の多変量相関散布図(図1)が基本的なグラフです。
図1は3組以上のデータ間の関係を一度に見られるようにしたもので「対散布図」とか「散布図行列」と呼ばれています(Pairs Scatter Plot)。
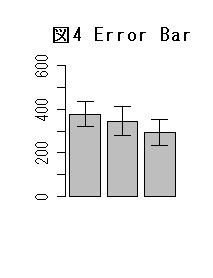
医学分野ではデータの平均値(あるいは中央値)やそのバラツキの違いをPlot Mean(図2)、Box Plot(図3)、Error Bar(図4)などで表します。
これらの散布図は複数の変量の分布をグラフ化したもので「Plot Mean と Error Bar」はパラメトリックの、そして、「Box Plot」はノンパラメトリックの統計記述として表現されます。
これらは同じ種類のデータの分布を比較するのに適しており、最近の探索的手法では Box Plot が多用されるようになって来ました。
データの特徴を捉える方法としては Bar Plot(棒グラフなど)などが基本ですが、CoPlot(2変量の散布図をグループごとに描き1つのグラフにしたもの)など色々と工夫された表現方法が開発されています。
Mat Plot(図5)は2つの行列の対応する列の散布図を一度に描くことが出来ます。また、分割表データの結果は Mosaic Plot (図6)で示されたりします。
この様に気の利いた美しいグラフは視覚的な効果が高く数字を羅列しただけの表よりも説得力があると思います。
いろいろな散布図を有効に使って分析結果を分かりやすく表現するのも統計的技術の1つかも知れません。
情報統計研究所に寄せられる依頼や相談で多い分析にロジスティック回帰分析が有ります。幾度かこのブログでも書いてきましたがもう一度、この分析をご紹介しておきたいと思います。分析の対象が「Control 群(0)/Patient 群(1)」など2値データで与えられているとき2項分布を仮定したロジスティック回帰分析が医学分野で幅広く用いられています。回帰式 logit(p)=log(p/(1-p)=b0+b1x1+b2x2+・・・・, に当てはめて p<=0.5 なら Control 群 とか p>0.5 ならPatient 群とかに判別します。
pの値は Z=b0+b1x1+b2x2+・・・・ , のとき、p=1/(1+exp(-Z) で求めます。
医学分野で多用されるのは、単に回帰式による判別だけが目的ではなく、ここでの p/(1-p) はオッズを表しています。したがって、推定された回帰係数(b1 , b2) の exp(b1) , exp(b2) はオッズ比となります。医学分野では回帰係数の有意性から有意変数を推定すると同時にオッズ比を知る事が出来るので多用されているのかも知れません。オッズ比の95%信頼区間は exp(b1±1.96*SE) から求めます(SE=回帰係数の標準誤差)。統計ソフトによっては exp(b1*(max-min)±1.96*SE)で出力されるものも有ります。回帰式による判別は cutoff 値を 0.5 として Control 群か Patient 群かを判別します。目的(従属)変数と説明(独立)変数が「0 と 1」のダミー変数であれば名義尺度かどうかを気にせず量的変数として扱うことが出来ます。しかし、統計ソフトによってはオッズ比の「0 に対する 1」の対数を回帰係数としている場合が有りますので、回帰式の判別(Cutoff=0.5 による)に気をつけて下さい。