統計のコツのこつ(56)

情報統計研究所をWeb上に開設して、間もなく、最初の依頼者は中学校の先生でした。分析結果の発表で賞を頂いたとか、また、ある医学学会の発表では人生初の１等賞を頂いただとか、大層お喜び頂いて恐縮すると共に、統計分析の重要性を改めて認識した次第です。さて、

前号(55)の続きで、回帰分析での外れ値についてです。
まずは、「R」環境で次のパッケージを事前にインストールしておいて下さい。
「robustbase」、「MASS」、「ggplot2」

 

そして、次のプログラムを実行しますが、データは前回の原データ"dat"です。

 

***
ibrary(robustbase)
fit.rob<- lmrob(dat$y~ dat$x, method="MM")　# ロバスト重回帰分析(lmrob：MM法)
summary(fit.rob)

 

library(MASS)
fit.rlm<- rlm(dat$y~ dat$x, method="MM")　# ロバスト重回帰分析(rlm：MM法)
stat<- summary(fit.rlm)
rr= data.frame(stat$coefficients)                           
rr$p.value = pt(rr$t.value, stat$df[2], lower.tail=FALSE)                     
rr
***

 

原データによるロバスト回帰分析の結果を表1と表2に示します。

 

表1　lmrob(MM法:積率法による推定値)の結果

------------------------------------------------------------------　
Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 0.004737   0.481313    0.01    0.992   
dat$x       7.384300   0.193199   38.22   <2e-16 ***

-----------------------------------------------------------------

 

表２ rlm(MM法:積率法による推定値)の結果

----------------------------------------------------------------------------　
                  Value Std..Error      t.value      p.value
(Intercept) 0.004707031  0.7132836  0.006599102 4.974037e-01
dat$x       7.384246485  0.3081548 23.962780398 2.081652e-15

----------------------------------------------------------------------------

 

回帰係数はよくにていますが、標準誤差に違いがあります。

次により、
標準誤差の違いを３方法の回帰直線(95％信頼区間)で見てみましょう。

***
library(ggplot2)
ggplot(data=dat, aes(x, y)) + geom_point() +
 geom_smooth(method = "lm", color = "black", level = 0.95) # lm法

ggplot(data=dat, aes(x, y)) + geom_point() +
 geom_smooth(method = "rlm", level = 0.95)　# rlm法

ggplot(data=dat, aes(x, y)) + geom_point() +
 geo

m_smooth(method = "lmrob", level = 0.95) # lmrob法
***

 

図１　lm法による95％信頼限界

 

 

図２　rlm法による信頼限界
 

 

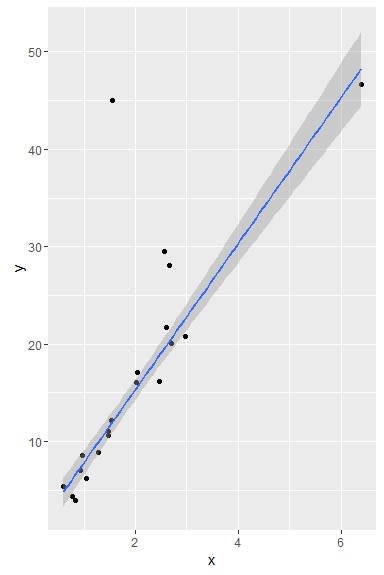
図３　lmrob法による信頼限界

 

ロバスト回帰分析は外れ値に小さな重みを与える統計手法と言えます。

"重み"は次により見ることが出来ます。

 

***
# lmrob法のweight

weights(fit.rob, type=c("robustness"))

 

出力結果：
         1          2          3          4          5          6          7
0.95918112 0.95355889 0.91893577 0.99990569 0.99913249 0.90772106 0.96249181
         8          9         10         11         12         13         14
0.97532552 0.00000000 0.98648925 0.99762937 0.99503501 0.99322134 0.06315755
        15         16         17         18         19         20
0.89642137 0.98025138 0.99947000 0.96902151 0.87153821 0.00000000
***

***
# rlmの法weight

fit.rlm$w

 

出力結果：
 [1] 0.95917520 0.95355297 0.91893080 0.99990484 0.99913013 0.90765097
 [7] 0.96246191 0.97529891 0.00000000 0.98647332 0.99763235 0.99503818
[13] 0.99323711 0.06295043 0.89639547 0.98023447 0.99946700 0.96902983
[19] 0.87144220 0.00000000
***

 

上記の出力結果(weight)から、原データの９行と２０行が除かれていることが分かります。すなわち、外れ値として除外された訳です。

ロバスト推定は普通の最小２乗法より複雑です。ここでは、ほんのサワリ程度のご紹介です。ただ単に、外れ値があるからと言ってロバスト回帰を無暗に用いるべきではないと思っています。

情報統計研究所はここから！

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

統計のコツのこつ(55)

 ずいぶんと間が空きました。学会の季節になると統計分析のご依頼やご相談や査読者への対応など立て込んで参ります。
当研究所は2000年にインターネット上で開設しましたが、当時、気軽に統計分析を利用できるWebサイトは少なかったと思います。お陰様で沢山の経験をさせて頂きました。分析費用が１桁違うのでは・・、と言われたりします。しかし、古い言葉かも知れませんが"苦学生"などの懐具合を思えば商売下手でいいと思ってやっています。

 

今回は、重回帰分析についてですが、通常(最小二乗法)の回帰分析ではなく「ロバスト回帰分析」について、その手法のほんの一例をご紹介したいと思います。

「すぐに役立つ統計のコツ」(オーム社)の94ページでは、普通(最小二乗法)の回帰分析しかご紹介していません。
そこで、
ガンマグロブリン(x)と反応する蛋白化学反応(y)の関係を例題にして、データ解析環境「R」での手法をご紹介します。

「R」の環境において、
新しいスクリプトを立ち上げ、次のプログラムを「コピー＆ペースト」して下さい。

***
Y<- c(4.3,6.2,16.2,11,7,17.1,8.5,16,29.5,12.1,10.6,8.9,46.7,28.1,3.9,5.4,20.1,20.8,21.7,45.0)
X<- c(0.77,1.04,2.46,1.48,0.92,2.03,0.97,2.02,2.57,1.53,1.48,1.27,6.4,2.67,0.83,0.6,2.7,2.98,2.6,1.56)

dat<- data.frame(y=Y, x=X)
dat # 原データの確認
***

 

外れ値(x=1.56, y=45.0)を除き"dat1"とします。
***
dat1<- dat[-20, ] # 原データから20行のデータを削除
dat1 # 外れ値を除いたデータの確認
***

 

原データ(dat)と外れ値削除後データ(dat1)の回帰直線を見てみましょう。
***
windows(width=4, height=6)
plot(dat$x, dat$y, pch=20, col="red", xlab="dat$x", ylab="dat$y")　# 外れ値（赤色）
par(new=T)
plot(dat1$x, dat1$y, pch=20,  xlab="", ylab="")
abline(lm(dat$y~ dat$x), lty=1, col="red")
abline(lm(dat1$y~ dat1$x), lty=1) # 外れ値の削除
***

 

図１　原データ(dat)と削除後データ(dat1)の回帰直線

 

 

図１の赤線は原データの、黒線は削除後の回帰直線です。

 

表１　削除後データ(dat1)によるlm法(普通の方法)の結果

----------------------------------------------------------
fit.lm<- lm(dat1$y~ dat1$x)
summary(fit.lm)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   0.2049     1.3947   0.147    0.885   
dat1$x        7.7762     0.5941  13.089 2.63e-10 

----------------------------------------------------------

 

次回は、
この原データを使って、「ロバスト回帰分析」をやって見ましょう。

 

次回（56）に続く！

 

情報統計研究所はここから。