JASPでベイズ統計のほんの一端をご紹介しましたが、今回の探索的因子分析(Exploratory Factor Analysis)で終わりとなります。
このブログでは、JASPの使用経験をチョットご紹介したに過ぎませんので、実際の分析では統計学的な方法にのっとり利用して下さい。
このブログでは、JASPの使用経験をチョットご紹介したに過ぎませんので、実際の分析では統計学的な方法にのっとり利用して下さい。
それでは、
前回のデータ「PCAdata.csv」での探索的因子分析の手順とその結果を示しておきます。
前回のデータ「PCAdata.csv」での探索的因子分析の手順とその結果を示しておきます。
JASP→File→Open→Computer→Browse(保存したホルダー)
↓
PCAdata.csv を開く
↓
すべての変数の尺度をScaleにする。
↓
Facter→Exploratory Factor Analysis
↓
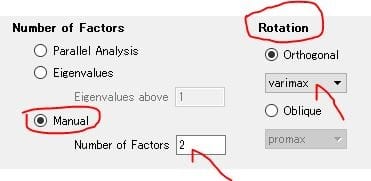
図1 各種設定(Rotation:none、Number of Facter[3])
↓
PCAdata.csv を開く
↓
すべての変数の尺度をScaleにする。
↓
Facter→Exploratory Factor Analysis
↓
図1 各種設定(Rotation:none、Number of Facter[3])

図2 回転なし(Rotation:none)での因子負荷量
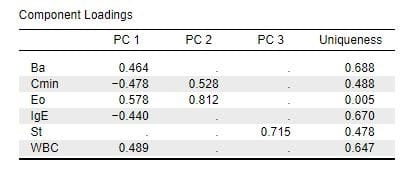
図2は因子数 [3]の時の負荷量で、
第1因子(PC1)のプラス負荷量[Ba, Eo, WBC] とマイナス負荷量[Cmin, IgE] にうまく分かれいるが、第3因子(PC3) はSt のみです。そこで・・・、
第1因子(PC1)のプラス負荷量[Ba, Eo, WBC] とマイナス負荷量[Cmin, IgE] にうまく分かれいるが、第3因子(PC3) はSt のみです。そこで・・・、
↓
図3 スクリープロット(Scree plot) を選択
図3 スクリープロット(Scree plot) を選択

Output options → ☑Scree plot としてスクリープロットを見てみよう。
↓
図4 因子数[3]の時のスクリープロット(Scree plot)
↓
図4 因子数[3]の時のスクリープロット(Scree plot)

このData の Scree plot は Components[3] から[4] の傾斜が平坦であるところから、因子数は[2]で良さそうです。そこで・・・、
↓
図5 因子数[2]で回転なし(Rotatio:none)の因子負荷量
↓
図5 因子数[2]で回転なし(Rotatio:none)の因子負荷量

各変数は第1因子と第2因子に分かれており、因子の意義付けが出来そうです。
因子の解釈には分析者の知識に依存し、説得できるだけの根拠が求められます。
ここで、
「Uniquenesis」は独自性とか独自因子と言われています。
因子の解釈には分析者の知識に依存し、説得できるだけの根拠が求められます。
ここで、
「Uniquenesis」は独自性とか独自因子と言われています。
また、
回転(Rotatio:varimax)にすると因子負荷量の分類がうまくゆきませんので、ここでのデータでは回転なし(Rotatio:none)が良さそうです。
回転(Rotatio:varimax)にすると因子負荷量の分類がうまくゆきませんので、ここでのデータでは回転なし(Rotatio:none)が良さそうです。
実際のデータでの因子分析では、因子数や回転など試行錯誤が伴います。JASPでは基本的な方法を簡単に色々と試せますが、専用ソフトには及びません。詳しい因子分析にはデータ解析環境「R]などの利用をお勧めします。
以上でJASPの使用経験のご紹介を終わります。
以後の投稿は未定ですが、例えば、
ニュースになった統計問題を取り上げてみようかと思ったりしています。
それでは又!!