医学と統計(96)

情報統計研究所へのアクセスはここから．

精度管理とYoudenplot(2)

前回は２つの値を ｘ軸と ｙ軸にとり、２つの値の相関散布図から系統誤差と確率誤差を視覚的に見る Youden plot を紹介しました。しかし、誤差に付いては数値として表現していません。たとえ、相関係数（ｒ）が大きいとか小さいとか言っても精度管理の指標としては曖昧なものです。系統や確率の誤差をAccuracy と Precion に対応付けるなら、管理図法で２つの値の変動をみると良いでしょう。

前回のデータで２つの値の trend をみてみましょう。


図１：Ａ法によるTrend 分析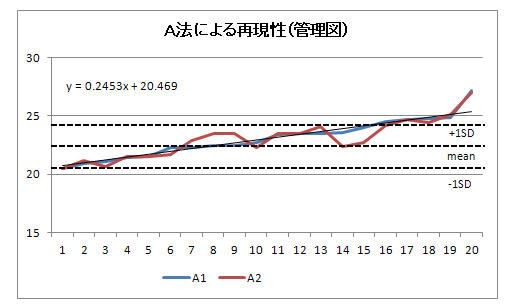


図２：Ｂ法によるTrend 分析


図１・２では、敢えて２つのデータを昇順順位にしています。

Ａ法（図１）とＢ法（図２）の trend は直線回帰式で表しており、その勾配係数は Ａ法＞Ｂ法 となっています。すなわち、Ａ法の勾配係数がＢ法に比べて大きく、Ａ法の 系統誤差（caliblation など）に問題が有るかも知れません。

同じ物質を測っていたとしても、ある程度の変動（ＣＶ%）は致し方ないものですが、なるべく小さくなるよう管理する必要があります。管理図法は日々の管理血清値の変化から確率誤差（バラツキなど）や系統誤差（システムなど）を把握するのに役立っています。

この様に、臨床検査の現場での精度管理は検査データを保証するものとして日常業務に欠かせないものです。しかし、この様な努力や精度管理の統計学的方法を知る臨床医は極く少ないかも知れませんよ・・・？

次回に続く！

医学と統計(95)

精度管理とYoudenplot について(1)。

臨床検査の現場では、特に生化学検査では日常的に精度管理が行われています。いわゆる、管理図法と言われるもので自動分析機の精度の指標として用いられています。
臨床検査における精度管理は長年の研究や経験から優れた方法が開発されています。今回、ここに紹介する「Youden plot（双値法）」は、特に目新しいものではありませんが、臨床検査のみならず色々な分野で役立つと思いますのでご紹介しておきます。
まずは、
精度管理用管理血清の仮想データを使ってみましょう。

Ａ法によるデータ
A1：20.5, 21.1, 21.5, 22.3, 22.7, 23.6, 20.9, 21.4, 23.5, 22.3, 23.5, 22.5, 22.5, 23.4, 24.0, 24.5, 24.8, 24.7, 24.9, 27.2
A2：20.5, 20.7, 21.5, 21.7, 22.3, 22.4, 21.2, 21.5, 23.5, 22.9, 24.1, 23.5, 23.5, 23.5, 22.7, 24.2, 24.4, 24.7, 25.1, 27.0

Ｂ法によるデータ
B1：21, 19.8, 21.0, 21.0, 20.5, 20.3, 21.5, 21.9, 21.0, 22.0, 20.8, 21.0, 21.0, 22.0, 22.1, 22.3, 22.0, 21.9, 21.0, 22.0
B2：19, 21.0, 21.0, 20.8, 21.0, 20.3, 21.8, 21.7, 21.0, 21.3, 20.6, 21.0, 22.0, 21.5, 22.5, 21.9, 21.9, 22.6, 23.7, 20.0

図１：Ａ法による Youden plot

横軸（x）はＡ１値、縦軸（Y）はＡ２値の散布図（相関係数 r=0.933、変動係数 CV=7.04%）。

図２：Ｂ法による Youden plot

横軸（x）はＢ１値、縦軸（Y）はＢ２値の散布図（相関係数 r=0.339、変動係数 CV=4.03%）。

図１と図２ において、実線の楕円形と円形は説明上、適当に描いたものです。実際には、90%又は95%信頼楕円や相関楕円あるいは 80%確率楕円を用いるのが良いかと思います。
要するに、
Ｘ軸とＹ軸の２つの値の相関が高ければ楕円形分布に、低ければ円形分布になります。
この例での、
図１は系統誤差（例えば、Caliblation の誤差など）が、図２は確率誤差（例えば、ランダムなバラツキ誤差など）が
疑われます。また、系統誤差は正確性（Accuracy）に、確率誤差は精密度（Precion）に対応づける様ですが、臨床検査のもろもろの誤差要因が複雑に絡みますので単純ではありません。

臨床検査値は日々の精度管理の努力によって信頼性が保障されています。

次回に続く。