情報統計研究所へのアクセスはここから．
統計ソフト「gretl」を使ってみよう(2)！
前回では「gretl」サイトから、
ダウンロードしたExcelファイル「MetaboData.xls」を Import し、「MetaboData.gdt」の名前で保存しました。
このgretl ファイルを用いてチョッとばかり医学に関連した統計メニューを試してみましょう。
File→Open data→User fiile→Open data→MetaboData.gdt
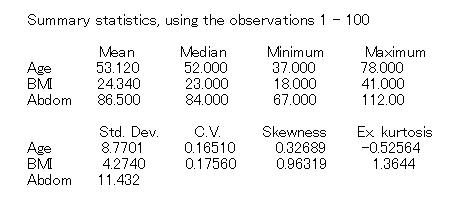
ファイルが呼び込まれました。各変数をダブルクリックすればデータを見ることが出来ます。
ここで、
「BM I」をクリックし、
Variable→ Box plot→ ◎Factorrized→ OK→ [ Metabo ]→ Factor(discrete)→ OK
とすれば、図１のBoxPlot（箱ひげ図）が出力されます。
図１ BM I のBoxPlot
同じ様に、変数「Abdom」をクリックし、
Variable→ Box plot→ ◎Factorrized→ OK→ [ Metabo ]→ Factor(discrete)→ OK
とすれば、図２のBoxPlot（箱ひげ図）が出力されます。
図２ Abdom のBoxPlot
図１と図２は「Metabo」（０＝メタボなし、１＝メタボあり）におけるBM I とAbdom（腹囲）の違いを示しています。
統計学的な検定（student's t-test、Wilcoxon sum rank test）は次により行うことが出来ます。
まず、
２群の既知の平均値と標準偏差によるBM I の 「Student's t-test」は、
Tools→ Test statistic calculator→ [ 2 means ]→
[ mean of sample 1=21.5 ], [ std. deviation, sample 1=2.215], [ size of sample 1=50]
[ mean of sample 2=21.5 ], [ std. deviation, sample 2=2.215], [ size of sample 2=50]
?Assume common population stadard deviation→OK
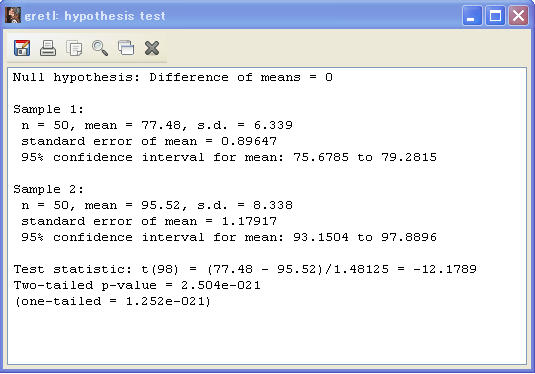
変数 Abdom の 「Student's t-test」は、
Tools→ Test statistic calculator→ [ 2 means ]→
[ mean of sample 1=77.48 ], [ std. deviation, sample 1=6.339], [ size of sample 1=50]
[ mean of sample 2=95.52 ], [ std. deviation, sample 2=8.338], [ size of sample 2=50]
?Assume common population stadard deviation→OK
平均差の検定結果は表１と表２に示す通りです（但し、Weioch t-test は出来ません）。
表１ BoxPlot（図１）の平均値差の検定結果
表２ BoxPlot（図２）の平均値差の検定結果
上記の方法は、２群（Metabo）の既知の平均値と標準偏差から計算したものですが、次の方法でも平均差の検定を行うことが出来ます。
変数[ Metabo]をクリックし、
Model→ Ordinary Least Squares→ [ BM I] 又は[ Abdom ]→ Dependent variable→OK
Ordinary Least Squares（最小２乗法）の結果は次の通りです。
表３ OLSによるBM I の結果 
表４ OLSによる Abdom の結果
表３と表４の「Log-likelihood」、「Akaike criterion」、「Schwarx criterion」、「Hannan-Quinn」は当てはめの良さを表す情報基準量です。
以上の結果から、
「Metabo」の有無による「BM I」と「Abdom」の平均値差が統計学的に高度に有意であることが分かりました。
ノンパラメトリック法でのWilcoxon の順位和検定 は、「Metabo」の「なし、あり」で２群に分けた２変数（BM I、Abdom）について、
「Toolｓ→ Nonparametric tests」
を行えば良いでしょう。
gretl でこの様なことも簡単に出来ます～ってことの一例です。
次回に続く！
