さて、
前回は「G*Power」によって一元配置分散分析(ANOVA)での効果量の求め方をご紹介しました。
今回は、もう少し詳しいANOVAでの出力結果を求めるために「データ解析環境 R」でやって見ましょう。
前回は「G*Power」によって一元配置分散分析(ANOVA)での効果量の求め方をご紹介しました。
今回は、もう少し詳しいANOVAでの出力結果を求めるために「データ解析環境 R」でやって見ましょう。
前回と同じ、
「すぐに役立つ統計のコツ:例題(表4.3)」で分散分析にける効果量など・・などを求めて見ましょう。
「すぐに役立つ統計のコツ:例題(表4.3)」で分散分析にける効果量など・・などを求めて見ましょう。
まず、
「R」を立ち上げ、パッケージ(rpsychi)をインストールしておいて下さい。
「R」を立ち上げ、パッケージ(rpsychi)をインストールしておいて下さい。
そして、
下記のコマンドを書き実行して下さい。
下記のコマンドを書き実行して下さい。
***
library(rpsychi)
library(rpsychi)
value<- c(
224,235,220,204,265,180,
186,190,235,181,225,155,
147,121,175,166,177,118
)
factor=factor(rep(c("A", "B", "C"), c(6, 6, 6)))
224,235,220,204,265,180,
186,190,235,181,225,155,
147,121,175,166,177,118
)
factor=factor(rep(c("A", "B", "C"), c(6, 6, 6)))
dat<- data.frame(VALUE=value, FACTOR=factor)
dat
dat
ind.oneway(VALUE~ FACTOR, data=dat)
出力結果:# 縦長にしたデータ
VALUE FACTOR
1 224 A
2 235 A
3 220 A
4 204 A
5 265 A
6 180 A
7 186 B
8 190 B
9 235 B
10 181 B
11 225 B
12 155 B
13 147 C
14 121 C
15 175 C
16 166 C
17 177 C
18 118 C
1 224 A
2 235 A
3 220 A
4 204 A
5 265 A
6 180 A
7 186 B
8 190 B
9 235 B
10 181 B
11 225 B
12 155 B
13 147 C
14 121 C
15 175 C
16 166 C
17 177 C
18 118 C
> ind.oneway(VALUE~ FACTOR, data=dat)
$anova.table # ANOVA表
SS df MS F
Between (A) 15330 2 7664.9 9.586
Within 11994 15 799.6
Total 27324 17
SS df MS F
Between (A) 15330 2 7664.9 9.586
Within 11994 15 799.6
Total 27324 17
# omnibus.es returns a omnibus effect size which is a η2, and it's confidence interval
$omnibus.es # イータ二乗とその95%信頼限界
etasq etasq.lower etasq.upper
0.561 0.127 0.717
etasq etasq.lower etasq.upper
0.561 0.127 0.717
# 前回の「η^2(イータの2乗)=SSa/SSt=0.561」と同じです。
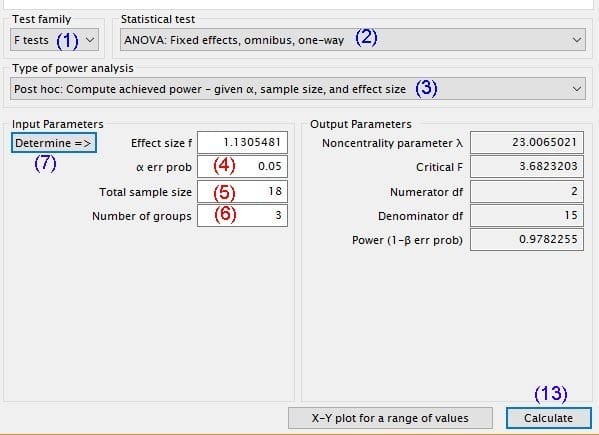
# F検定の標本効果量 f <- sqrt( SSa / SSe ) =√(グループ間の変動/グループ内の変動)=√(15330/11994)=1.131
# 回帰分析の標本効果量 η2 = SSa / SSt=グループ間の変動/全体の変動=15330/27324=0.561(56.1%)
# F検定の標本効果量 f <- sqrt( SSa / SSe ) =√(グループ間の変動/グループ内の変動)=√(15330/11994)=1.131
# 回帰分析の標本効果量 η2 = SSa / SSt=グループ間の変動/全体の変動=15330/27324=0.561(56.1%)
= R2=決定係数
# 確かに、ややこしいので論文などでは注意して下さい。
# 確かに、ややこしいので論文などでは注意して下さい。
$raw.contrasts
mean.diff lower upper std
1-2 26.000 -8.798 60.798 16.326 # 投薬前と2カ月後の平均値の差
1-3 70.667 35.869 105.464 16.326 # 投薬前と4カ月後の平均値の差
2-3 44.667 9.869 79.464 16.326 # 2カ月後と4カ月後の平均値の差
mean.diff lower upper std
1-2 26.000 -8.798 60.798 16.326 # 投薬前と2カ月後の平均値の差
1-3 70.667 35.869 105.464 16.326 # 投薬前と4カ月後の平均値の差
2-3 44.667 9.869 79.464 16.326 # 2カ月後と4カ月後の平均値の差
# std=標準誤差と呼ばれ、「sqrt(MS_within*(1/n1+1/n2))=799.6*(1/6+1/6)=16.326」です。
$standardized.contrasts
es lower upper std
1-2 0.919 -0.311 2.15 0.577
1-3 2.499 1.268 3.73 0.577
2-3 1.580 0.349 2.81 0.577
es lower upper std
1-2 0.919 -0.311 2.15 0.577
1-3 2.499 1.268 3.73 0.577
2-3 1.580 0.349 2.81 0.577
# コントラスト(Hedges's g)の標準化平均差、母集団標準化平均差の近似信頼区間、および標準誤差
# Hedgesのg = 平均値の差/√MSe=26/sqrt(799.6)=0.919
# Hedgesのg = 平均値の差/√MSe=26/sqrt(799.6)=0.919