前回は、「すぐに役立つ統計のコツ」(オーム社)の106ページ(ロジスティック回帰分析)から、イベント(反応値)などが度数の場合のロジスティック回帰分析についてご紹介しました。
ロジスティック回帰分析と関連したものに「プロビット(probit)」があります。
これについては、
下記URLの「統計学入門」(杉本典夫先生)に詳しいので見て下さい。
これについては、
下記URLの「統計学入門」(杉本典夫先生)に詳しいので見て下さい。
http://www.snap-tck.com/room04/c01/stat/stat13/stat1304.html
それでは、
統計学入門(第13章4)の「表13.4.1 名義尺度の時の用量反応試験のデータ」を用いて「R」でやってみましょう。
筆算での計算過程を見たいなら「統計学入門(第13章4)」の手法をたどって下さい。
ここでは、
データ解析環境「R」での方法をご紹介します。データは次のように書き表すことが出来ます。
統計学入門(第13章4)の「表13.4.1 名義尺度の時の用量反応試験のデータ」を用いて「R」でやってみましょう。
筆算での計算過程を見たいなら「統計学入門(第13章4)」の手法をたどって下さい。
ここでは、
データ解析環境「R」での方法をご紹介します。データは次のように書き表すことが出来ます。
***
res1<- c(0,2,16,15,19) # 反応数
res0<- c(20,18,14,5,1) # 非反応数
dose<- c(0.01,0.1,1,10,100) # 用量
res1<- c(0,2,16,15,19) # 反応数
res0<- c(20,18,14,5,1) # 非反応数
dose<- c(0.01,0.1,1,10,100) # 用量
log.dose<- log10(dose) # 常用対数に変換
fit1<- glm(cbind(res1, res0)~ log.dose, family = binomial(probit))
summary(fit1)
summary(fit1)
出力結果:
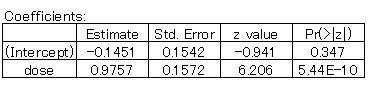
***
切片(Intercept)の出力値が「統計学入門(第13章4)」の値と違っていますが、
次により修正して下さい「統計学入門(第13章4)参照」。
次により修正して下さい「統計学入門(第13章4)参照」。
***
5+fit1$coefficients[1]
5+fit1$coefficients[1]
切片(Intercept)の値:
> 5+fit1$coefficients[1]
(Intercept)
4.854886
***
> 5+fit1$coefficients[1]
(Intercept)
4.854886
***
このプロビットモデルでD50を求めてみましょう。
***
library(MASS)
ld.dose<- dose.p(fit1, p = 0.5 )
10^ld.dose # 常用対数から変換
library(MASS)
ld.dose<- dose.p(fit1, p = 0.5 )
10^ld.dose # 常用対数から変換
出力結果:
.............Dose........SE
p = 0.5: 0.1487214 0.1572426
p = 0.5: 0.1487214 0.1572426
D50 = 10^0.1487 ≑ 1.408 g/Kg
***
***
ここで、
LD50の95%CI(信頼区間)は関数「attr」を使って次により知ることが出来ます。
LD50の95%CI(信頼区間)は関数「attr」を使って次により知ることが出来ます。
***
dose.SE<- attributes(log.dose)$SE
lower <- log.dose - dose.SE * 1.96
upper <- log.dose + dose.SE * 1.96
lower
upper
dose.SE<- attributes(log.dose)$SE
lower <- log.dose - dose.SE * 1.96
upper <- log.dose + dose.SE * 1.96
lower
upper
出力結果:
> lower
Dose SE
[1,] -0.1594741 0.1572426
> lower
Dose SE
[1,] -0.1594741 0.1572426
> upper
Dose SE
[1,] 0.4569169 0.1572426
D50の95%信頼区間は次の通りです(常用対数をもどす)。
D_lower~D_upper=10^-0.159471~10^0.4569169=0.6926692g/Kg~2.86363g/Kg
<<「統計学入門(第13章4)」の値と多少違っています>>
情報統計研究所はここから!









