このブログは「すぐに役立つ統計のコツ」(オーム社)をもとに書いています。

今回は本書(114p)の判別分析についてご紹介します。
本書の「例題19」では腎障害患者を"慢性糸球体腎炎患者"と"尿細管障害患者"の2群に判別する方法として、ロジスティック回帰分析による判別分析をご紹介しています。
すなわち、独立変数の効果に注目した判別方法と言えます。しかし、
今回ここでは、データ解析環境「R」の関数式を用いた線形判別分析をご紹介します。例題は、
本書の「例題19」では腎障害患者を"慢性糸球体腎炎患者"と"尿細管障害患者"の2群に判別する方法として、ロジスティック回帰分析による判別分析をご紹介しています。
すなわち、独立変数の効果に注目した判別方法と言えます。しかし、
今回ここでは、データ解析環境「R」の関数式を用いた線形判別分析をご紹介します。例題は、
本書(例題19)のデータに「U.BGM(尿中β2-Microgloburin)」を加えた表1のデータを使って見ましょう。
表1 腎障害患者のExcelデータ
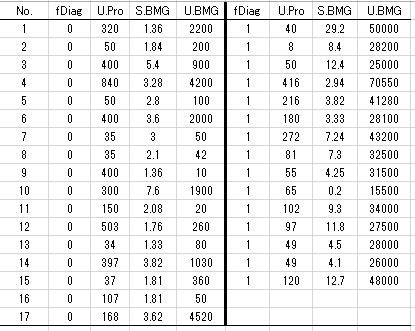
表1 の Excelデータを表2の様に縦長のフォームに加工し、コピー&ペーストで「R」に取り込みます。
表2 縦長にしたデータのフォーム

(fDiag の「0:慢性糸球体腎炎患者、1:尿細管障害患者」としています)
「R」プログラムの実行
***
dat<- read.delim("clipboard", header=T) # データの取り込み
head(dat)
s.dat<- scale(dat[, 2:4]) # データの標準化との違いをみるため
dat1<- cbind(dat, s.dat) # 原データと標準化データの結合
head(dat1) # 結合データの確認
dat<- read.delim("clipboard", header=T) # データの取り込み
head(dat)
s.dat<- scale(dat[, 2:4]) # データの標準化との違いをみるため
dat1<- cbind(dat, s.dat) # 原データと標準化データの結合
head(dat1) # 結合データの確認
y1<- dat1[, 1] # 目的変数(fDiag)
x1<- dat1[, 2] # 説明変数(U.Pro)
x2<- dat1[, 3] # 説明変数(S.BMG)
x3<- dat1[, 4] # 説明変数(U.BMG)
x1<- dat1[, 2] # 説明変数(U.Pro)
x2<- dat1[, 3] # 説明変数(S.BMG)
x3<- dat1[, 4] # 説明変数(U.BMG)
library(MASS) # パッケージを事前にインストールしておく
z1<- lda(y1~ x1+ x2+ x3, CV=F) # lda関数による判別分析(CV=Fは交差確認なし)
z1<- lda(y1~ x1+ x2+ x3, CV=F) # lda関数による判別分析(CV=Fは交差確認なし)
z1
出力結果:
Call:
lda(y1 ~ x1 + x2 + x3, CV = F)
lda(y1 ~ x1 + x2 + x3, CV = F)
Prior probabilities of groups:
0 1
0.53125 0.46875
0 1
0.53125 0.46875
Group means:
x1 x2 x3
0 248.5882 2.857059 1054.235
1 120.0000 8.098667 35288.667
x1 x2 x3
0 248.5882 2.857059 1054.235
1 120.0000 8.098667 35288.667
Coefficients of linear discriminants:
LD1
x1 -0.0030586273
x2 -0.0146857850
x3 0.0001160874
***
LD1
x1 -0.0030586273
x2 -0.0146857850
x3 0.0001160874
***
よって判別式は、
z1=-0.0030586273*U.Pro- 0.014685785*S.BMG+ 0.0001160874*U.BMG- c0
z1=-0.0030586273*U.Pro- 0.014685785*S.BMG+ 0.0001160874*U.BMG- c0
となります。ここで、c0 は次により求めることが出来ます。
c0<- apply(z1$means%*%z1$scaling,2,mean)
c0=1.465343
c0=1.465343
上記で求めた判別得点と下記の判別得点は若干異なる様です・・。
実際には、次により判別結果を求めることが出来ます。
***
predict(z1)$x # 判別得点
predict(z1)$class # 判別されたグループ
round(predict(z1)$posterior,3) # 事後確率
lda.tab<- table(dat[, 1], predict(z1)$class)
lda.tab # 判別結果
Correct<- sum(lda.tab[row(lda.tab)==col(lda.tab)])/sum(lda.tab)*100 # 判別率(%)
Correct
100-Correct # 誤班別率(%)
***
predict(z1)$x # 判別得点
predict(z1)$class # 判別されたグループ
round(predict(z1)$posterior,3) # 事後確率
lda.tab<- table(dat[, 1], predict(z1)$class)
lda.tab # 判別結果
Correct<- sum(lda.tab[row(lda.tab)==col(lda.tab)])/sum(lda.tab)*100 # 判別率(%)
Correct
100-Correct # 誤班別率(%)
***
ここで、未知のデータでの求め方の一例です。
***
# 未知データの判別
# 未知データの判別
newdata<- rbind(c(320,1.36,2200),c(120,12.7,48000))
dimnames(newdata)<- list(NULL, c("U.Pro","S.BMG","U.BMG"))
newdata<- data.frame(newdata)
predict(z1, newdata=newdata)
dimnames(newdata)<- list(NULL, c("U.Pro","S.BMG","U.BMG"))
newdata<- data.frame(newdata)
predict(z1, newdata=newdata)
***
なお、
標準化したデータを使うなら次のようにして下さい。
標準化したデータを使うなら次のようにして下さい。
***
y12<- dat1[, 1] # 目的変数(fDiag)
x12<- dat1[, 5] # 標準化した説明変数(U.Pro)
x22<- dat1[, 6] # 標準化した説明変数(S.BMG)
x32<- dat1[, 7] # 標準化した説明変数(U.BMG)
y12<- dat1[, 1] # 目的変数(fDiag)
x12<- dat1[, 5] # 標準化した説明変数(U.Pro)
x22<- dat1[, 6] # 標準化した説明変数(S.BMG)
x32<- dat1[, 7] # 標準化した説明変数(U.BMG)
z12<- lda(y12~ x12+ x22+ x32, CV=F)
z12
z12
***
また、非線形判別分析は次の関数があります。
***
zq<- qda(y1~ x1+ x2+ x3, data=dat)
zq
***
zq<- qda(y1~ x1+ x2+ x3, data=dat)
zq
***
ここで、
z1(z12)の CV を CV=T とした場合は"交差確認"の結果を得ます。
これに付いては、
「統計学入門、杉本典夫 先生」(第1章8)を参考にして下さい。
z1(z12)の CV を CV=T とした場合は"交差確認"の結果を得ます。
これに付いては、
「統計学入門、杉本典夫 先生」(第1章8)を参考にして下さい。
http://www.snap-tck.com/room04/c01/stat/stat01/stat0108.html
次回は、SPSS(正準判別分析)でやって見ましょう。
情報統計研究所はここから!









