このブログは「すぐに役立つ統計のコツ」(オーム社)で書き足らなかった事柄を書いています。
今回は、「クラスター分析」のいくつかの方法をデータ解析環境「R」を使ってご紹介します。
今回は、「クラスター分析」のいくつかの方法をデータ解析環境「R」を使ってご紹介します。
それでは、「すぐに役立つ統計のコツ」第7章(117ページ)を開いて下さい。
本書の「例題 20」(表7.24)は情報統計研究所(HP)の「著書の正誤表と例題」の[Excel Samples]をクリックし、[Excel Sample(2)]をダウンロードして下さい。
[Excel_Sample(2).xlsx](Sheet名:表7.25)の「A1~E7」を「選択→コピー」し「R」に
取り込んで下さい。要領は統計のコツのこつ(16)と同じです。
それでは[R]を立ち上げて下記のコマンドを実行して下さい。
***
dat<- read.delim("clipboard", header=T)
head(dat)
dat<- read.delim("clipboard", header=T)
head(dat)
# 2種類のデンドログラム(樹形図)の作成
# ユークリッド距離(complete:完全連結法とか最遠隣法と言う)
# ユークリッド距離(complete:完全連結法とか最遠隣法と言う)
plot(hclust(dist(dat, "euclidean"), "complete"), hang=-1)
# ユークリッド距離(Ward法:ウォード法とか最小分散法とも言う)
plot(hclust(dist(dat, "euclidean"), "ward.D"), hang=-1)
出力結果:
図1:最遠隣法
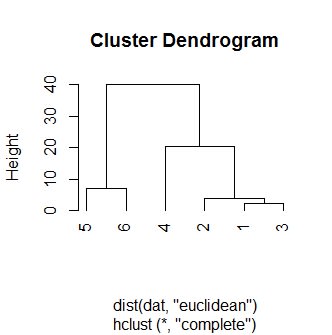
図2:ウォード法
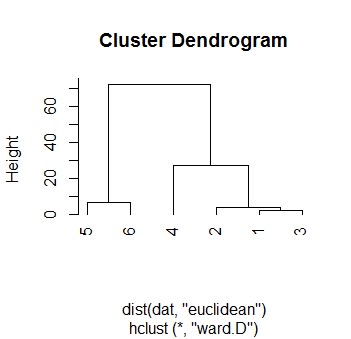
その他の方法を実行される場合は、次の様な引数を使って下さい。
単連結法(最近隣法):single
群平均法 :verage
重心法 :centroid
メディアン法 :median
McQuitty法 :mequitty
群平均法 :verage
重心法 :centroid
メディアン法 :median
McQuitty法 :mequitty
クラスター分析の実例として、情報統計研究所(http://kstat.sakura.ne.jp/index003_2.htm)を参考にして下さい。
図3:学力考査のデンドログラム(一例)

図4:民力指標のデンドログラム(一例)

次も引き続き「多変量解析(主成分分析、124ページ)」のお話です。