情報統計研究所.(統計分析のご相談ご依頼)のアクセスはここから。
移動平均と時差相関係数について。
図1 のデータは気管支喘息患者の末梢血中好塩基球数(Ba) と血清IgE値の日差変動の時系列データです。
図1 Ba と IgE の時系列データ
このデータの移動平均(7日)は図2 ( Ba )と図3 ( IgE )のように、Ba も IgE も増加と上昇の傾向が見られます。
図2 Ba の移動平均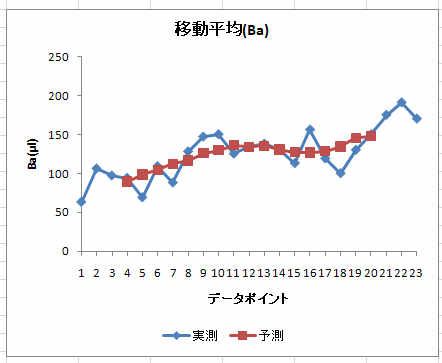
図3 IgE の移動平均
移動平均はMSエクセルの「データ分析→分析ツール→移動平均」を利用すれば良いでしょう。ここでは、
時差相関(相互相関とも言う)について説明したいと思います。時差相関はBa と IgE のデータを一つずつずらして相関係数を求めたものです。図4 の時差系列を見て下さい。
図4 Ba と IgE の時差系列
図4 の様に、時差相関は対応する時系列データを一つずつずらせた青色部分の相関係数を求めたものです。時差相関係数はMSエクセルの関数を用いて計算することが出来ます(Microsoft Office Excel2007)。関数式による計算は次により行うことも出来ます。最初に、
Ba と IgE は測定単位が違いますので標準化をおこなっておきます。すなわち、
Ba を Xi とするとき dXi = ( Xi - meanX )/SDx
IgE を Yi とするとき dYi = ( Yi - meanY )/SDy
を求めておき( SD=標準偏差 )、
Sxx = SUMSQ ( DXi )^0.5 、Syy = SUMSQ ( DYi )^0.5
から、
Lag=1 のとき、Sxy = SUMPRODUCT( X1: X22 , Y2 : Y23 )
Lag=2 のとき、Sxy = SUMPRODUCT( X1: X21 , Y3 : Y23 )
:
Lag=10 のとき、Sxy = SUMPRODUCT( X1: X13 , Y11 : Y23 )
を求めます。以上から、
時差10日( Lag time=10 ) の時差相関係数は、次により求められます。
r(k) = Sxy(k) / Sx(0)・Sy(0) ( k=1, 2, ・・・, 10)
ここで注意すべきは、
Sx と Sy は時差=0 を用います(過去には、単純に Sxy(k)/Sx(k)・Sy(k) で求めたものもあります)。
次回に続く!













