それでは、
前回の続きでベイズによる相関分析をやってみましょう。
前回の続きでベイズによる相関分析をやってみましょう。
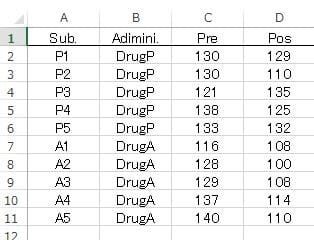
例題は、前回の「ZTT-Protein.csv」を使います。
初めての方は、
前回のブログを見て情報統計研究所からデータをダウンロードして下さい。
前回のブログを見て情報統計研究所からデータをダウンロードして下さい。
JASPの実行:
*****
「ZTT-Protein.csv」の読込
↓
Regression アイコン
↓
Beyesian Correlation Matrix
↓
「ZTT と a2Glb」を選択し、この関係を見てみましょう。
↓
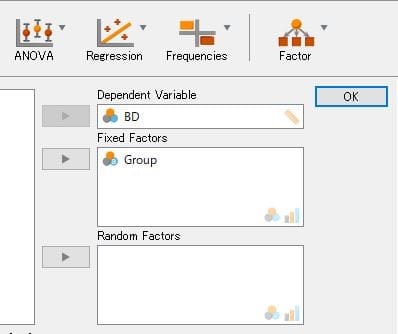
図1 分析方法の選択
*****
「ZTT-Protein.csv」の読込
↓
Regression アイコン
↓
Beyesian Correlation Matrix
↓
「ZTT と a2Glb」を選択し、この関係を見てみましょう。
↓
図1 分析方法の選択
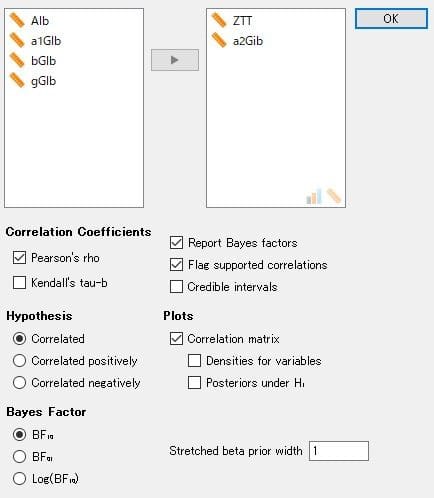
図1の仮説検定を任意に選択してみて下さい。
◎ Correlated positivity:正の相関に関する検定結果を見る。
◎ Correlated positivity:負の相関に関する検定結果を見る。
◎ Correlated positivity:負の相関に関する検定結果を見る。
↓
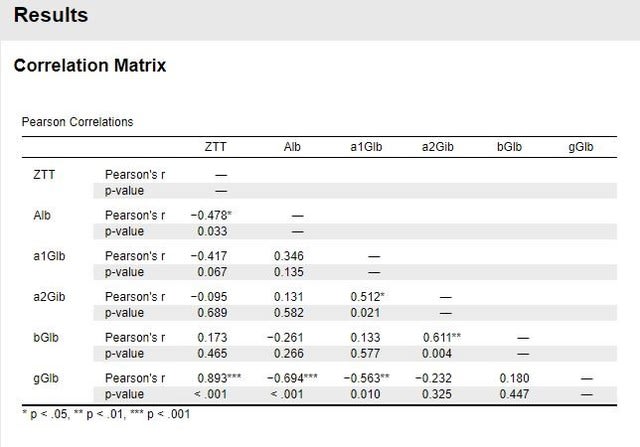
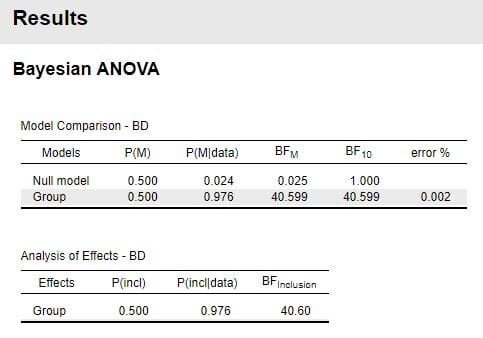
図2 分析結果(相関行列)
図2 分析結果(相関行列)

「Pearson's r=-0.095, BF10=0.298」で相関関係は非常に弱い様です。
↓
図3 分析結果(相関散布図)
図3 分析結果(相関散布図)

相関散布図と回帰直線が示されています。
それでは、
「ZTT と gGlb」の関係はどうでしょうか?
↓
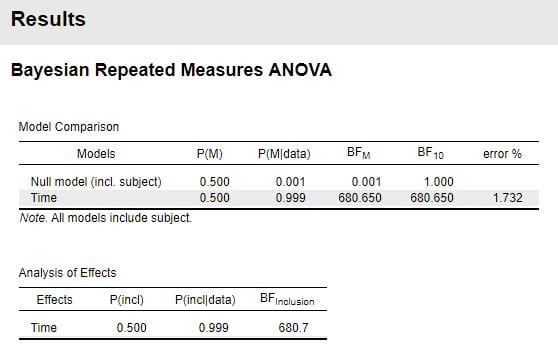
図4 分析結果(ZTT:gGlbの相関行列)
「ZTT と gGlb」の関係はどうでしょうか?
↓
図4 分析結果(ZTT:gGlbの相関行列)

「Pearson's r=-0.893, BF10=116453」で相関関係は非常に強い様です。
相関の強さは、BF10の[*]~[***]マークを見れば見当がつくでしょう。
相関の強さは、BF10の[*]~[***]マークを見れば見当がつくでしょう。
↓
図5 分析結果(相関散布図)
図5 分析結果(相関散布図)

「ZTT と gGlb」の直線関係が分かります。
ここで、
Regression → Bayesian Correlation Pairs
↓
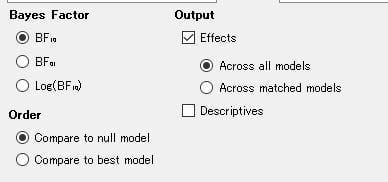
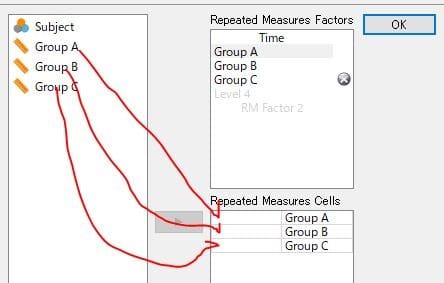
図6 事前・事後の分布の選択
Regression → Bayesian Correlation Pairs
↓
図6 事前・事後の分布の選択

赤矢印を選択してみて下さい。
↓
図7 事前・事後の分布
図7 事前・事後の分布

「事前(Prior)の一様分布と事後(Posterior)」の分布が示されます。
↓
図8 帰無仮設(H0)と対立仮設(H1)の図示
図8 帰無仮設(H0)と対立仮設(H1)の図示

BF10とBF01の値と、事後分布のmedian=0.862, 95% CI [0.699, 0.955]が表示されると共に「dataH1:dataH0」の関係がイラストで示されています。
その他、
「Linear Regression」、「Baysisian Linear Regression」も同じ要領で色々と試してJASPの機能を確かめて下さい。
「Linear Regression」、「Baysisian Linear Regression」も同じ要領で色々と試してJASPの機能を確かめて下さい。
次回に続く!
情報統計研究所はここから。