情報統計研究所へのアクセスはここから．
名義ロジスティック回帰分析のコツ
名義変数が「０,１」のデータについて、「SAS-JMP」と「R」でのチョトしたコツみたいなものを
ご紹介したいと思います。
データは統計解析環境「R」の "libraly(MASS)" の 「birthwt」 を用いて見ましょう。
「R」から 「birthwt」 データは次により取り出して下さい。
library(MASS)
dat<- birthwt
dat
面倒あるいは不慣れであれば、
下記のURLから編集データを downloard して下さい。
http://www3.ocn.ne.jp/~stat/dbase/dbase.html
（「出産時体重」を右クリックし "対象ファイルを保存" で 「BirthWeight.xls」 を読み込む）
各変数は次の様に説明されています。
low ： 出産時体重2.5Kg、名義（以上＝0、未満＝1））
indicator of birth weight less than 2.5 kg.
age ： 母親の年齢、量的
mother's age in years.
lwt ： 母親の体重、量的
mother's weight in pounds at last menstrual period.
race ： 母親の人種、名義（白人＝１、黒人＝２、その他＝３）
mother's race (1 = white, 2 = black, 3 = other).
smoke ： 妊娠中の喫煙、名義（無＝０、有＝１）
smoking status during pregnancy.
ptl ： 早産の回数、量的（０回＝０、１回＝１、２回＝２、３回＝３）
number of previous premature labours.
ht ： 母親の高血圧の有無、名義（無＝０、有＝１）
history of hypertension.
ui ： 子宮過敏性の有無、名義（無＝０、有＝１）
presence of uterine irritability.
ftv ： 削除します
number of physician visits during the first trimester.
bwt ： 出生時体重、量的
birth weight in grams.
「R] で取り出したデータは一旦、MS-Excell で編集しておくことをお勧めします。
まずは、
便利な 「SAS-JMP」 で基本統計量を求めて見ましょう。
出産時体重（g）
min 25%tile median 75%tile max mean(sd)
--------------------------------------------------------------------------------
709 2412 2977 3515.5 4990 2944.6(729.2)
図１ 出産時体重のヒストグラムと比率(JMP の出力結果)
次に、
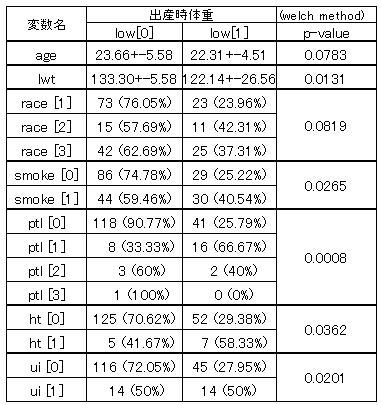
表１の単変量の結果を見て見ましょう （ この様な分析にはJMPがとても便利です ）。
表１ 単変量分析結果
母親の年齢（age）と母親の体重（lwt）は対数変換で正規分布に近似させてからの方が良いのですが、商用統計ソフトの普及でノンパラメットリック分析が容易となり、正規分布にこだわらない傾向が見られます。しかし、歪みも程度によりますので、分布の形状を見る習慣が肝要かと思います。
名義ロジスティック回帰分析を JMP で行うには、「 BirthWeight.xls 」 の JMP データの様に 「R」データと逆の「0 , 1」になっています。
JMP の 「 列(c)→値のチェック→リストチェック 」 で 「0」 が上位になっていますので、「 0／1 」の関係、すなわち、「 0 に対する 1 」の回帰関係となります。このデータでは 2.5 Kg 未満に対するものですから、「JMP」では 「R」 と逆になります。
文字データであれば 「 リストチェック 」 で変更出来ますが、いちいちの変更は手間ですので、「母親の人種（race）」のダミー化も「 MS-Excel 」でやっておきます。
名義ロジスティック回帰分析の結果
表２ 「JMP]での結果
表３ 「R」での結果
（frace2、frace3 は race をファクター化したダミー変数）
「JMP」と「R」の推定値が異なっていますが、これは表４の関係による「JMP」の独自性ですので尊重しましょう！？（表4）。
表４ 範囲オッズ比、単位オッズ比の計算式
尺度 (範囲)オッズ比 単位オッズ比
連続 Exp(β(Xmax-Xmin)) Exp(β)
名義 Exp(2β) Exp(β)
順序 Exp(β) Exp(β)
次回は、
このデータを使って「ベイジアンネットワーク」によるグラフィカル分析を紹介したいと思います。