統計のコツのこつ(30)

このブログは「すぐに役立つ統計のコツ」(オーム社）に紹介されている内容に沿って書いています。
本書を参考にお読みいただければ分かり易いかと思います。

それでは、本書の第３章（10ページ）を開いて下さい。
この章では、２つの標本の平均値の検定について書いていますが、もし、２つの平均値を併合する必要があったら、どうすれば良いでしょうか・・・、正規分布に従う事を前提に、その計算方法をご紹介しましょう。

例えば、
データ解析環境「R」で「平均値(mean)＝100、標準偏差(sd)＝10」の正規分布のデータを100個作ってみます。

 

***
n<- rnorm(100, mean=100, sd=10)
n
***

 

この100個の平均値と標準偏差は、 mean(sd)＝100.29(10.49)となりました。

 

次により、100個のデータを n1=70、n2＝30 の２つに分けて見ましょう。

 

***
x<- as.matrix(n)
x1<- x[1:70, ]
x2<- x[71:100, ]
x1
x2
***

x1は n1＝70、 mean(sd)＝99.19(10.03)
x2は n2＝30、 mean(sd＝102.85(11.24)

 

となりました。

 

この２つの平均値と標準偏差を併合して見ましょう。

併合は、図１のExcel の関数式で行えば容易に、図２の結果を得ることが出来ます。

 

図１　平均値の併合のための関数式

 

図２　平均値の併合の結果

 

 

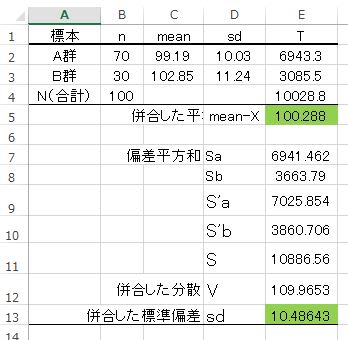
（緑色セルに併合した平均値と標準偏差が出力されます）

 

計算式は、
情報統計研究所のホームページ「やさしい医学統計手法」を見て下さい。

URL
http://kstat.sakura.ne.jp/medical/med_001.htm

（「2.3.3.平均値・分散の結合」をクリックして下さい）

 

それでは、
次回も「すぐに役立つ統計のコツ」(オーム社）からチョットした事柄をご紹介したいと思います。

 

情報統計研究所はここから！

 

 

 

 

統計のコツのこつ(29)

明けましておめでとう御座います。
今年も、本稿を続けて行きたいと思っていますので、どうぞよろしくお願い致します。

それでは、

「すぐに役立つ統計のコツ」(オーム社）の９ページ(下段の図)を見て下さい。

 

ここで紹介している"Notch Box Plot"はBox(箱)のNotch(ノッチ)が中央値の95％信頼区間(95%CI)となります。
しかし、
９ページの図ではノッチがハッキリしませんので次の図１で説明しましょう。

 

図１　BoxPlotとNotch BoxPLot

 

図１は前回と前々回の"年齢と性別"のデータから、"年齢"について通常の"Box Plot"と"Notch Box Plot"を作成したものです。

図１において"Notch"は赤線で示しており、この矢印の区間が"中央値の95%CI"となります。

それでは、
この"95%CI" はどの様にして求めるのでしょうか・・。

データ解析環境「R」を使えば簡単です。

例えば、前回、前々回の"年齢と性別"のデータであれば、

 

***

dat<- read.delim("clipboard", header=T)
head(dat)

library(askio) # 事前にパッケージをインストールしておく
ci.median(dat$Age, conf = 0.95)

 

出力結果：

95% Confidence interval for population median
Estimate     2.5%    97.5%
      70       68       72

***

 

すなわち、
図１の Notch の部分(95% CI)は「68～72」と言うことです。

これは、
データ(Age)を昇順順位に並べ替えたときの、「21番目と36番目」の"Age"になります。

簡単な近似方法としては、次により求めることが出来ます。

median±1.57×IQR／√n＝70±1.57×8／√56＝68.32～71.68 (IQR：四分位偏差)

 

一方、
Excelなどでの筆算では、
統計学入門第３章（杉本典夫 先生）をご参照下さい。
http://www.snap-tck.com/room04/c01/stat/stat03/stat0302_1.html

 

引用文
***
中央値の100(1-α)％信頼区間は正規分布の100α％点の値t(∞,α)を用いて次のようになります。
r=(n+1)／2－t(∞,α)×r√n／2 (切り捨てによって整数化する)
***

 

 

それでは、今年も引き続き掲載の予定ですので、よろしくお願いします。

 

情報統計研究所はここから！