統計技術 第Ⅲ部：第3章-2：Multiple Regression（重回帰分析）

統計技術 第Ⅲ部　Free Online Caluclator （例題集）
第3章-2：Multiple Regression（重回帰分析）

ここでの重回帰分析は、２つ以上の独立（説明）変数と従属（目的）変数の関係を多項方程式　
　Y＝ｂ1X1+ｂ2X2+・・・b0

で表す多変量分析の１つである．

使用する Free Online Calculator ：
● Free Statistics Software (Calculator) - Web-enabled scientific services & applications 
 https://www.wessa.net

上記URLのトップページから、
↓
Regression Software
↓
Multiple Regression
↓
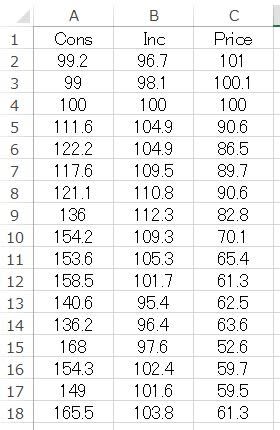
図１　Data X と Names of X columns: などの規定値を確認

↓
Compute をクリック

出力結果
--------------------------------------
図2　重回帰式（推定式）

図３　重回帰推定パラメータ

図４　重回帰統計量


図５　多重共線性の検定

ここでの多重共線性は検出許容値（tolerance）または分散拡大係数（VIF）を用いている．
 tolerance=1-Rj^2    VIF=1/tolerance

詳しくは、下記URL（統計学入門：杉本典夫）を参考にされたい．
 http://www.snap-tck.com/room04/c01/stat/stat07/stat0702.html

また、下記URL「Gooブログ：医学と統計（44）(45)」に例題を示している．
医学と統計（44）
 https://blog.goo.ne.jp/k-stat/e/7a9a0624fd14b888be1add8b4156d48d

ここで、
Rj^2 は、説明変数を他のすべての説明変数に回帰したときの決定係数であり、0.20または0.10未満、あるいは VIFが ５以上であれば、多重共線性が疑われる．
Farrar–Glauber 検定は変数が直交していれば多重共線性はないと判断し、直交していなければ、少なくともある程度の多重共線性があると判断する．

#「R」での実行：
# 既定値（Data X） を選択し、Excelにコピーしワークシートにペーストして利用すれば便利である．
----------------------------------------------------------
dat<- read.delim("clipboard", header=T) # データの読み込み
dat　# データの確認
fit1<- lm(a ~ b + c , data=dat)
summary(fit1)

library(car)
vif(fit1)

# 別法
library(mctest)
fit2<- lm(a ~ b + c , data=dat)
summary(fit2)

#　統計量
id<-imcdiag(fit2); id$idiags[,1]

# VIFの閾値を「5 」としたとき．
imcdiag(fit2, method = "VIF", vif = 5)
----------------------------------------------------------
別法の出力結果：

図６　R（mctest）の統計量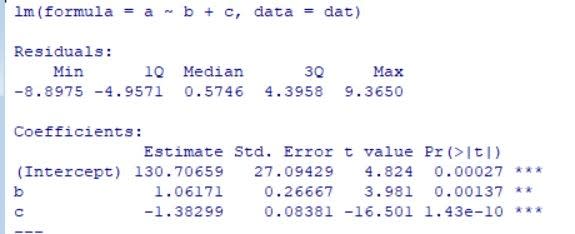


図７　R（mctest）によるVIF閾値＝５での判定

# 1 --> COLLINEARITY ”あり”と判定
# 0 --> COLLINEARITY ”なし”と判定

----------------------------------------------------------
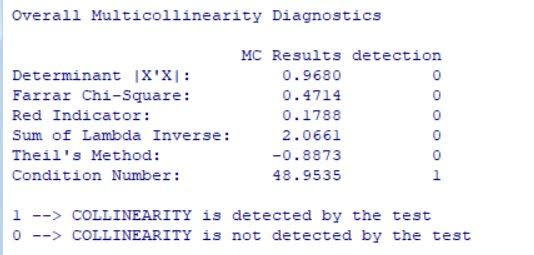
# Farrar–Glauber test:
omcdiag(fit2, detr=0.001, conf=0.99)
omcdiag(fit2)[1]
----------------------------------------------------------
Farrar–Glauber testの結果

統計技術 第Ⅲ部: 第3章 Regression Software(回帰分析)

統計技術 第Ⅲ部　Free Online Caluclator （例題集）

第3章　Regression Software （回帰分析）
　ここでは、単回帰分析及び複数の回帰分析タイプ（方程式）の分析法を紹介する．複数の回帰方程式としては、下記の様な方法である．

● Multiple Regression
● Logistic Regression
 computes the Bias-Reduced Logistic Regression model as proposed by David Firth
 バイアス低減ロジスティック回帰（Firthメソッドによる）．
参照
http://toukei.sblo.jp/article/188015481.html

● Regression Trees
 カテゴリ変数と連続変数からなるデータの分類木ーと回帰木の計算
● PLS-PM
 部分的な最小二乗によるパスモデルの計算

第3章-1：Simple Regression （単回帰分析）
　単回帰分析での方程式は Y=a + bX であり、2次元座標上において、Y はY軸上にある従属変数（目的変数）、X は軸上にプロットされる独立変数（説明変数） 、bはYの勾配、そして、a はYの切片である．
よって、統計では単純な線形回帰で、１つの説明変数でもって表す線形回帰モデルである．つまりは、1つの独立変数と 1つの従属変数を持つ２次元座標上の関係から、その線形関数（直線性）を見つけ、独立変数から従属変数を予測することであり、簡単に言えば、結果変数（Ｙ）が １つの因子（Ｘ）に関連しているということを示すものである．

使用する Free Online Calculator ：
● Free Statistics Software (Calculator) - Web-enabled scientific services & applications 
 https://www.wessa.net

上記URLのトップページから、

Simple Regression を選択
↓
既定値（Data X） を確認
↓
変数名（Names of X columuns） を確認
↓
Response Variable：従属（目的）変数
↓
Explanatory Vriable：独立（説明）変数
↓
Include Intercept Term（切片を含む）
↓
Compute をクリック

出力結果
--------------------------------------
図１　直線回帰モデル（Y=IQ、X=Add）

Y=-0.667*X+135.163、R^2=0.396 （調整R^2=0.389）

図２　分散分析表

p-value<0.0001（有意）

図３　散布図（回帰直線）

Excel での方法
--------------------------------------
既定値（Data X） を選択しコピー
↓
Excel のワークシートにペースト

図４　Excel 形式のデータ

↓
データ→データ分析→回帰分析
↓
図５　入力元などを指定

図６　Excelによる出力結果

 

第2章-4：Multivariate Descriptive Statistics （続き）

統計技術 第Ⅲ部：第2章 多変量記述統計（7）
第2章-4：Multivariate Descriptive Statistics （続き）
(3) Agglomerative Nesting(Hierarchical Clustering)

● Free Statistics Software (Calculator) - Web-enabled scientific services & applications 
 https://www.wessa.net

上記サイトから、簡単な例題をやってみよう．

Descriptive Statistics→Multivariate Descriptive Statistics
↓
● Agglomerative Nesting(Hierarchical Clustering)を選択
↓
図1　データをセット（既存のデータと入れ替える）


Names of X column: [ Pollen Temple Humidity Weather ]とする．
↓
Compute をクリック
↓
凝集型階層的クラスタリング（Kaufman and Rousseeuw）の計算結果が出力される．
↓
(Lance-Williams formular は既定値のまま)
↓
出力結果(1)
Agglomerative Nesting ( Hierarchical Clustering )
Agglomerative Coefficient=0.7909976
（この係数が大きいほど蜜である）
↓
図１　出力結果(2)

euclidean（ユークリッド距離）、average（平均法）によるデンドログラフが出力される．

階層クラスタリング（AHC ：Agglomerative Hierarchical Clustering）は凝集型（ボトムアップ型：bottom-up clustering　とも言う）であり、多くは非類似度（距離のような場合）に基づいて計算される．

ここで、
データ解析環境「R」での方法を見てみよう．
下記のコマンドを実行する．
---------------------------------
 Pollen<- c(4.3,2.2,4.6,11.1,29.9,36.5)
 Temple<- c(4.1,5.1,6.2,6.8,14.2,14.9)
 Humidity<- c(77,74,76,58,58,56)
 Weather<- c(3,3,3,2,2,2)
 dat <- data.frame(Pollen, Temple, Humidity, Weather)
 dat
 library(cluster)
# Compute agnes()
 Res<- agnes(dat, diss=FALSE, metric="euclidian", method = "average")
# Agglomerative coefficient
 Res$ac
# Plot the tree using pltree()
 pltree(Res, cex = 0.6, hang = -1, main = "Dendrogram of Agnes") 
---------------------------------
なお、　
観測データの単位が異なるときは標準化をおこなって検討することがある，
その時は、stan=TRUE"として実行すればよい．
---------------------------------
 Res<- agnes(dat, diss=FALSE, stan=TRUE", metric="euclidian", method = "average")
---------------------------------

なお、一般的な方法として、
● Hierarchical Clustering を選択すれば、
階層的クラスター分析とは、個体間の類似度あるいは非類似度 (距離) に基づいて、最も似ている個体から順次に集めてクラスターを作っていく方法である。個体間の類似度あるいは非類似度 (距離) に基づいて、最も似ている個体から順次にクラスターを作られる．
↓
図２　階層的クラスター分析によるデンドログラム

「R」では下記のコマンドを実行する．
---------------------------------
 Pollen<- c(4.3,2.2,4.6,11.1,29.9,36.5)
 Temple<- c(4.1,5.1,6.2,6.8,14.2,14.9)
 Humidity<- c(77,74,76,58,58,56)
 Weather<- c(3,3,3,2,2,2)
 dat <- data.frame(Pollen, Temple, Humidity, Weather)
 dat

plot(hclust(dist(dat, "euclidean"), "average"), hang=-1)
---------------------------------

 

第2章-4：Multivariate Descriptive Statistics (続き)

統計技術 第Ⅲ部：第2章 多変量記述統計（6）
第2章-4：Multivariate Descriptive Statistics （続き）

● Free Statistics Software (Calculator) - Web-enabled scientific services & applications 
 https://www.wessa.net

(２) Notched Boxplots
一般的なBoxplots（箱ひげ図）の変形であり、四分位数の数値で標本の広がりや歪度をグラフィカルに示したものである．
ノッチ（Notch）とは、中央値からの95％信頼区間（95%CI）を箱の切れ目（ノッチ）で示しており、例えば、2群のNotchが重ならないなら統計的に有意（p<0.05）と判断される．

それでは、例題を実行してNotched Boxplotsをみてみよう．

「Wessa.net」のTop ページから、
　Descritive Statistisc を選択
↓
下方にスクロースして、
Multivariate Descriptive Statistics 
↓
既存のデータ
↓
Compute をクリック

図１　Boxplot statics

lower(upper) whisker, hinge, median の統計量表示．

図２　Boxplot Nitches

lower(upper) bound, median の統計量表示

図３　Notched Boxplots


図４　Notched Boxplots （whisker, hinge, median, bound) の説明

ここで、
図１の統計量をまとめると次のようになる．

....Variable.....lower/upper whisker.....lower/upper hinge.....median
........A...................99/168..................117.6/154.2.........136.2
........B................95.4/112.3................98.1/105.3...........102.4
........C................52.6/101...................61.3/90.6..............70.1

....Variable.....lower/upper bound
........A................122.17 
........B..................99.64
........C..................58.72

なお、
lower/upper whisker は 最小値/最大値又は%tile内の値を用いることが多い．
lower/upper hinge    は 25%/75% tile(3rd quartile)に一致することが多い．
lower/upper bound   は median±1.58*IQR/√n
 IQR=upper hinge (75%tile)- lower hinge (25%tile)

 

統計技術 第Ⅲ部：第2章 多変量記述統計（５）

統計技術 第Ⅲ部：第2章 多変量記述統計（５）
第2章-4 Multivariate Descriptive Statistics （多変量記述統計）

ここでは、複数変量（多変量）におけるケンドールのタウ順位相関、スピアマンの順位相関、ピアソン相関などを一括して求めることが出来る．
ただし、多変量回帰分析、すなわち、従属変数（目的変数）に対する複数の独立変数（説明変数）の関係をみるものではない．
それでは、
Wessa.net 事例集から下記について紹介する．
　（１）Kendall tau Correlation Matrix
　（２）Notched Boxplots

● Free Statistics Software (Calculator) - Web-enabled scientific services & applications 
 https://www.wessa.net

「Wessa.net」のTop ページから、
　Descritive Statistisc を選択
↓
下方にスクロースして、
Multivariate Descriptive Statistics 
↓
Kendall tau Correlation を選択
↓
図１　データ入力画面


図２　出力結果：相関関係（Pearson r）

Excel では、CORREL()関数で求めることが出来る．

図３　出力結果：相関関係（p-value）

ここでは、ピアソン相関、ケンドールのタウ順位相関、スピアマンの順位相関．

図３　出力結果：相関関係（Scatter Plots）

表記の数値は相関係数ではな（p-value）．

データ解析環境「R」では、Excel に入力されたデータ（図４）をコピー・ペーストし下記の「R」コマンドを実行すれば良い．

図４　Excel に入力されたデータ形式の場合

図４の列名を含むデータをすべて選択しコピーして「R」に読み込む．
-------------------------------------------
# コピーしたデータの読み込み
　dat<- read.delim("clipboard", header=T)
　dat

　x<-dat$Cons
　y<- dat$Inc
　z<- dat$Price
# ピアソン相関
　cor(x, y, metho="pearson")
　cor(x, z, metho="pearson")
　cor(y, z, metho="pearson")
# スピアマンの順位相関
　cor(x, y, metho="spearman")
　cor(x, z, metho="spearman")
　cor(y, z, metho="spearman")
# ケンドールのタウ順位相関
　cor(x, y, metho="kendal")
　cor(x, z, metho="kendal")
　cor(y, z, metho="kendal")
------------------------------------------
同じ結果がえられる．

次回の（２）Notched Boxplots に続く・・．