統計のコツのこつ(42)

「すぐに役立つ統計のコツ」(第5章、40ページ)はカテゴリカルデータ(計数データ)・・・、名義尺度データについて紹介しています。

そして、
量的データをカテゴリカルデータに変換(ダミー変数 ０,１を付与)し、分割表形式の統計的方法や検定方法について説明しています。

ここでは、
データ解析環境「Ｒ」での操作についてご紹介します。

まず、
例題として、下記URL(情報統計研究所)にアクセスして下さい。

　http://kstat.sakura.ne.jp

 

TOP ページから、[Excel Sample]をクリック、[Excel Sample(1)：表22～表5.19]をダウンロードし、Sheet名「表5.3」を開くと、本書(表5.3、42ページ)のデータを得ることが出来ます。

 

このデータを用いて「Ｒ」での操作をやってみましょう！

 

「Ｒ」を立ち上げ、

・「R Console」 の画面に、
      dat<- read.delim("clipboard", header=T)

 

と記載し、実行せずにおいて下さい。そして、
　　
・「Excel_Sample(1).xlsx」（Sheet名「表5.3」）の「Ｊ列２行：Ｏ列102行」を選択しコピーします。

 

そして、
・「R Console」 の画面の、
　　dat<- read.delim("clipboard", header=T)

 

を実行しすれば、データを取り込む事が出来ます。

確認は次により行えば良いでしょう。

 

head(dat)　# データの確認

 

そして、

 

・「Ｒ」→ファイル→新しいスクリプト
・新しいスクリプトの「無題・Ｒエディタ」に以下のプログラムを書き実行します。
・関数「table()、ftable()、xtabs()」を使って見ましょう。

 

***
attach(dat)
C.table1<- table(Gender, TC) # table()による２×２分割表
C.table1

C.ftable1<- ftable(Gender, TC) # ftable()による２×２分割表
C.ftable1

C.xtable1<- xtabs(~ Gender + TC) # xtabs()による２×２分割表
C.xtable1

 

round(prop.table(C.table1), 3)    # 全体の合計に対する比率
round(prop.table(C.table1, 1), 3) # 行の　合計に対する比率
round(prop.table(C.table1, 2), 3) # 列の  合計に対する比率

 

# 「ftable1」と「xtabs」も同じで、全体に対する比率は次のようにします。

 

round(prop.table(C.ftable1), 3)   
round(prop.table(C.xtable1), 3)

 

出力結果：
次のような２×２分割表が出力されます。

            TC 
Gender  0      1
   0       32    11
   1       54      3
***

 

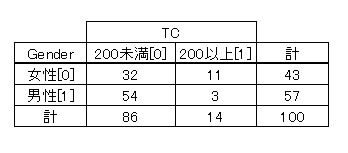
この出力結果を選択・コピーし、MS-Excel にテキスト・ペーストして整形すれば図１の様な分割表を作ることが出来ます。

 

図１　GenderとTC の分割表

 

 

なお、カイ二乗計算は次により行えば良いでしょう。

 

***
chisq.test(C.table1, correct = T) 　 # 補正あり(既定値)
chisq.test(C.table1, correct = F) 　 # 補正なし
chisq.test(C.table1, simulate.p.value = T、B = 2000)
      # モンテカルロ・シュミレーションの計算と試行回数

 

fisher.test(C.table1)       # フイッシャーの直接確率計算
***

 

長くなりますので、今回はここまでとします。

次回は「R」でピボットテーブルをご紹介したいと思います。

なお、
本書の表5.16(49ページ)のデータは加工したもので、「Excel_Sample(1).xlsx」とは一致しません。

 

情報統計研究所はここから！

 

 

 

 

 

 

 

 

 

統計のコツのこつ(41)

ここしばらくは、「すぐに役立つ統計のコツ」では触れていない効果量(ES)や検出力(Power)の求め方をご紹介して来ました。

ES や Power の筆算でのキーワードは「非心ｔ分布」です。これを筆算するのはやっかいですが、幸いにも"CASIO" の電卓??(下記URL)を使えば楽ちんです。

 

http://keisan.casio.jp/keisan/service.php

 

やってみましょう！

上記URL画面より、
［専門的な計算］→［統計関数］→［非心ｔ分布］→［非心ｔ分布］を選択

 

***
http://keisan.casio.jp/exec/system/1161228870

 

非心ｔ分布の確率密度、下側累積確率、上側累積確率を求めます。
***

 

図１ 未入力画面　

 

 

図１の画面で次により計算した値を入力します。

・パーセント点(x)：t(α, df)
・自由度(v)：n1+n2-2
・非心度(λ)：es × √(n1*n2/(n1+n2))

 

例えば、
２つの平均値の差(対応なし)の検定データから、次の値から Power を求めて見ましょう。

n1 = 30             
n2 = 20              
効果量d = 0.954      
有意水準α = 0.05

 

まずは、下記の筆算を行います。

 

***
● 自由度(v)＝30＋20－2＝48
● パーセント点(x)＝ｔ（0.05, 48)＝2.0106：（注１）
● 非心度(λ)＝0.954×√30×20／(30＋20）＝3.3047

 

注１：
ｔ分布のパーセント点は、
［専門的な計算］→［統計関数］→［スチューデントのｔ分布（パーセント点）］→

[累積確率：0.025, 自由度：48]→[2.0106]

 

として求めれば良いでしょう。
***

 

そして、
上記の値をそれぞれ図２の様に入力し[計算](６桁に変更)をクリックすると、図２の結果が得られます。

 

図２ 入力と計算結果の画面　

 

 

上側累積確率の値(0.8994)が Power(1-β)＝89.94% となります。

 

では、
次の「対応あり」のデータをやって見ましょう。

 

n = 101                           
効果量d = 0.322      
有意水準α = 0.05

 

***
●自由度(v)＝101-1＝100
●パーセント点(x)＝ｔ（0.05, 100)＝1.984
●非心度(λ)＝0.322×√101＝3.236
***

 

上側累積確率の値(0.893) が Power(1-β)＝89.3% となります。

 

*******************
統計のコツのこつ(40)に対するコメントをご紹介します。

 

杉本典夫 先生のコメント要旨

 

対応の無いt検定(一元配置分散分析)と対応の有るt検定の違いは、前者が2群の平均値の差が0かどうかを検定するのに対して、後者が変化量平均値が0かどうかを検定する点です。そのため「一般的には有意差の出やすい方法を採用」するのではなく、時期変動を検討するための評価指標として、平均値の差が妥当なのか、それとも変化量平均値が妥当なのかで使い分けるべきです。僕のサイト(http://www.snap-tck.com/room04/c01/stat/stat03/stat0303.html)にこのことを端的に表す例を挙げてあるので参考にしてください。

 

情報統計研究所はここから！

 

 

 

 

 

 

統計のコツのこつ(40)

前回の「統計のコツのこつ(39)」でご紹介した例題は誤解を招く恐れがありますので、言い訳みたいですが、説明させて頂きます。

統計のコツのこつ(36)～(39)までは、一元配置分散分析(ANOVA)における効果量の求め方についてご紹介してきました。
しかし、
例題は同一被験者の薬剤投与前後における値ではないか・・、だとすれば、これは「対応のある検定」を適用するべきだ・・、と言うことです。
すなわち、
各被験者の「投与前と投与後」の"平均値の差"ではなく、"差の平均値"が有意であるかどうかです（一般的には有意差の出やすい方法を採用します）。

ごもっともですが、
この例題では、対応を考慮せず（前後の変化量＝前後差を比較せず）に平均値差の検定と効果量の求め方をご紹介しました。

対応する２標本の有意差検定については、
「すぐに役立つ統計のコツ」の「第３章：4.対応する２標本のの有意差検定(21ページ)」や「第７章：二元配置分散分析(100ページ)」、あるいは、「やさしい医学統計手法」(http://kstat.sakura.ne.jp/medical/med_016.htm)を参考にして下さい。

 

この様な誤解を避けるためにも、論文などでは「対応のあるt検定(Paired t-test)」と記載しておくと良いでしょう。

 

前回の「統計のコツのこつ(39)」では、効果量計算サイトで、

「2.Comparison of groups with different sample size(Cohen's d, Hedges' g)」

 

を選択しましたが、

「対応のあるt検定」を用いるときは、
「4.Calculation of d from the test statistics of dependent and independent t-tests」

 

を用いて下さい。

 

その結果は次の通りです。

***
Mode of testing [dependent]
Student t value [6.1052     ] # Paired t-test の値
n1                   [6              ]
r                     [0.472        ] # 相関係数
 
Effect Size d     [2.561       ]

 

なお、
「G*Power」から求めたPower(1-βerror prob)＝0.997(99.7%)でした。
***

 

貴重なるご指摘に感謝致します。

 

 

統計のコツのこつ(39)

前回の続きです。
今回は無料のWebサイト(効果量計算サイト)を利用し、「すぐに役立つ統計のコツ」(31ページ、表4.1)の「投与前と４か月後」を例題にしてみましょう。

データは次のように要約されています。

　　　　投与前　   4か月後
  n           6             6
mean  　221.3　　150.7
 sd          28.68      26.39

 

計算サイトの1例として、下記のURLにアクセスして下さい。

 

https://www.psychometrica.de/effect_size.html#cohenb

 

Top 画面：

 

 

効果量計算の選択（No.2 を選択）：

 

 

統計量の入力画面：

 

 

効果量（Effect Size d_cohen）＝2.562
効果量の95％信頼限界＝1.035～4.089

 

なお、
「G*Power」から求めたPower(1-βerror prob)＝0.9784(97.84%)でした。

 

その他にも色々なサイトがありますの、自己責任でご利用されたらいかがでしょうか・・・。

 

その他、Webサイトの１例：

 

http://www.uccs.edu/~lbecker/

http://www.socscistatistics.com/effectsize/Default3.aspx

このブログは、統計手法の一端をご紹介しているに過ぎません。
詳しい統計学的な内容は専門書などで学習して欲しいものです。

情報統計研究所はここから！

 

統計のコツのこつ(38)

このブログは「すぐに役立つ統計のコツ」をもとに書いています。
統計分析は「習うより慣れろ・・！」ではないかと思っています。難しそうな統計学を一から始めるよりも、まずはやって見ましょう。
最近は、色々な無料の統計ソフトや著名な商用統計ソフトの試用版などが容易に使えますので、本書の内容をなぞってみては如何ですか。

このブログでは、無料の統計ソフトとMS-Excelでの方法を中心にご紹介しています。

それでは本題です。

「すぐに役立つ統計のコツ：表4.9（37ページ）」を見て下さい。

 

Kruskal Wallis テスト(K-W test)において、厳密にはバラツキが等しいかを調べます。参考までにその「R」での方法をご紹介しておきましょう。

前回のデータ（一元配置分散分析）の出力結果（縦長にしたデータ）を用いて試して下さい。

 

「R」での方法

***
fligner.test(VALUE ~ FACTOR, data=dat)　# Fligner-Killeen（フリグナー・キリーン）
kruskal.test(VALUE ~ FACTOR, data=dat)

 

出力結果：

 

Fligner-Killeen test of homogeneity of variances

data:  VALUE by FACTOR
Fligner-Killeen:med chi-squared = 0.003643, df = 2, p-value = 0.9982

 

# p-value から、有意と言えませんので「バラツキは等しい」と判断します。

# 参考までに、Kruskal-Wallis test の結果は次の通りです。
# 「すぐに役立つ統計のコツ：表4.9（37ページ）」参照。

 

Kruskal-Wallis rank sum test

data:  VALUE by FACTOR
Kruskal-Wallis chi-squared = 10.312, df = 2, p-value = 0.005765
***

 

さて、
ここで一元配置分散分析(ANOVA)であれ、K-W test であれ、有意であればすべての組み合わせか、あるいは、どれかの組み合わせにおいて有意差があると言えます。それを調べるのが多重比較です。

「すぐに役立つ統計のコツ」(第４章、29ページ)では、ノンパラメトリック法の「ホルム・ボンフェローニ」とパラメトリック法の「チューキのＨＳＤ」について説明しています。

 

本書では記載していませんが、多重比較でも効果量の記載が求められる様になってきましたので、例題でご紹介しておきましょう。例題は、
前回と同じ「すぐに役立つ統計のコツ：例題(表4.1、31ページ)」です。

まずは、
「統計のコツのこつ(36)」でご紹介した検出力分析ソフト「G・Power」でやってみましょう。

 

●「GPower」による手順「統計のコツのこつ(36)参照）」

例えば、
本書(表4.1)の「投与前と２か月後」の効果量を求めて見ましょう。

 

test family→t-test→Mean：Wilcoxon-Mann-Whitney(two group)→Post hoc
　[Tail(s)：Two、Sample size group 1 = 6、Sample size group 2 = 6]→Determine→

　◎ n1=n2[Mean group 1 = 221.3, Mean group 2 = 195.3, SD group 1 = 28.68, SD group 2 = 29.67]

→Calculate and transfer to main window→Calculate

 

出力結果：
　Effect size d = 0.891、Power = 0.2738(27.38%)

 

注釈：
効果量(Effect size)はLarge(0.80以上）なのに、検出力(Power)は小さい。すなわち、効果量に見合ったデータ数で無い様です。下記のMann-Whitney U-test からも有意でないことが p-value から分かります。

 

***
 Mann-Whitney U-test  
 U = 11.5 , E(U) = 18 , V(U) = 38.86364  
 z-value = -1.043  
 p-value = 0.297107  
***

 

効果量を表す指標は色々あり、正直に言ってどの指標を用いるべきか迷う時もあります。しかし、大きく分ければ
　・Cohen's d ：平均値の差を標準化した効果量（d famiky：ｄ族）
　・r ：相関関係の強さ(association：r family：ｒ族）

 

の２種類が多用されていると思います。

 

長くなりましたので、「r family」の計算は次回にします。

それから、
この例題は「パラメトリック検定」のものを用いて紹介しています（念のため・・・）。

 

 

情報統計研究所はここから！