今回はデータや統計的記述の視覚的な表現である散布図(Scatter Plot)について紹介します。散布図としては2変量の関係を見る2組の相関散布図や3組以上の多変量相関散布図(図1)が基本的なグラフです。
図1は3組以上のデータ間の関係を一度に見られるようにしたもので「対散布図」とか「散布図行列」と呼ばれています(Pairs Scatter Plot)。
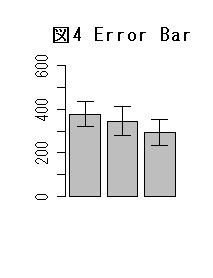
医学分野ではデータの平均値(あるいは中央値)やそのバラツキの違いをPlot Mean(図2)、Box Plot(図3)、Error Bar(図4)などで表します。
これらの散布図は複数の変量の分布をグラフ化したもので「Plot Mean と Error Bar」はパラメトリックの、そして、「Box Plot」はノンパラメトリックの統計記述として表現されます。
これらは同じ種類のデータの分布を比較するのに適しており、最近の探索的手法では Box Plot が多用されるようになって来ました。
データの特徴を捉える方法としては Bar Plot(棒グラフなど)などが基本ですが、CoPlot(2変量の散布図をグループごとに描き1つのグラフにしたもの)など色々と工夫された表現方法が開発されています。
Mat Plot(図5)は2つの行列の対応する列の散布図を一度に描くことが出来ます。また、分割表データの結果は Mosaic Plot (図6)で示されたりします。
この様に気の利いた美しいグラフは視覚的な効果が高く数字を羅列しただけの表よりも説得力があると思います。
いろいろな散布図を有効に使って分析結果を分かりやすく表現するのも統計的技術の1つかも知れません。