東京消防庁no17

1～5の番号が書かれた5つのボールを青色、赤色、黄色の3つの箱に入れる場合の数と、区別のつかない5つのボールを区別のつかない3つの箱に入れる場合の数の差として、最も妥当なのはどれか。ただし、5つのボールはすべて、いずれかの箱に入れるものとする。 1. 180 2. 197 3.204 4. 221 5.238 　　　　　　　　　　　　　　　すべての箱に最低1個はボールを入れるものとする、という問題はよくあるが、5つのボールはすべて、いずれかの箱に入れるものとする、という条件は、あまり見たことがありません。たとえば、①のボールはどの箱にも入れないなど、あまり考えたりしません。つまり、この条件は、「全てのボールは必ずどれかの箱に入れる」という、当たり前のことをいっているだけです。よって、この問題を考えるときには、空になる箱があってもあっても構わない。 前者は、重複順列なので、3の5乗で、243通り。（①は、青か赤か黄色かで3通り。②も、同様に3通り。③も④も⑤も3通り。その結果、空の箱ができても、こっちの知ったことではない。）後者は、何個入りの箱が何種類できるかだけを聞いています。一番多い箱をa,2番目に多い箱をb,一番少ない箱をc（同じ個数もあり）とすると、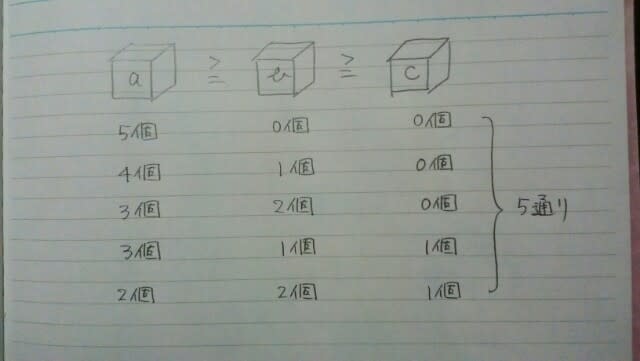よって、その差は、243－5＝238通り。5が正解。